Gpedia, вашата енциклопедия
Теоремата на Щайнице комбинаторно описание на неориентирани графи, образувани от ръбовете и върховете на 3D изпъкнал полиедър - те са точно (прости) равнинни графи, свързани с върхове 3 (с поне четири върха) [1] [2] . Тоест всеки изпъкнал политоп образува 3-свързана равнинна графа и всяка 3-свързана равнинна графа може да бъде представена като изпъкнал политоп. Поради тази причина 3-свързаните равнинни графи се наричат още многостенни [3] .
Името "теорема на Щайниц" е приложимо и за други резултати на Щайниц:
- лемата за заместване на Щайниц[en] — че всеки базис на векторно пространство има еднакъв брой вектори [5] ;
- теоремата, че ако изпъкналата обвивка на набор от точки съдържа единична сфера, тогава съществува крайно подмножество от точки, чиято изпъкнала обвивка съдържа по-малка концентрична сфера [6] ;
- векторно обобщение на теоремата за прегрупиране на Риман на Щайниц за условно конвергентни серии [7][8][9][10] .
Съдържание
Твърдение на теоремата
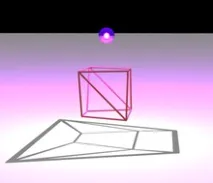
Неориентираният граф е система от върхове и ръбове, като всеки ръб свързва два върха. График може да бъде образуван от всеки полиедър, ако върховете на графиката се приемат за върхове на полиедъра и два върха на графиката са свързани с ребро, ако съответните върхове на полиедъра са крайните точки на неговите ръбове. Тази графика е известна като едномерен скелет на многостена.
Една графика е равнинна, ако нейните върхове могат да бъдат поставени върху равнина и ръбовете на графиката могат да бъдат начертани върху тази равнина като криви, свързващи тези точки, по такъв начин, че нито един ръб не се пресича и върховете лежат на такива криви, ако само върхът е краенточка на съответния ръб. Чрез теоремата на Фари можем да приемем, че кривите всъщност са сегменти. Един граф е vertex-3-sween, ако след премахване на всеки два от неговите върхове всяка двойка от останалите върхове може да бъде свързана с път.
Твърдението на теоремата на Щайниц в една посока (по-лесно за доказване) казва, че графиката на всеки изпъкнал политоп е равнинна и 3-свързана. Както е показано на фигурата, равнинността може да бъде показана с помощта на диаграма на Шлегел - ако поставите точков източник на светлина близо до една от страните на полиедъра и поставите равнина от другата страна, сенките на ръбовете на многостена образуват равнинна графика, вградена в равнината по такъв начин, че ръбовете на графиката са представени като сегменти. 3-свързаността на графика на политоп е специален случай на теоремата на Балински, че графиката на всекиk-мерен изпъкнал политоп еk-свързан [11] .
Твърдението по друг, по-сложен начин казва, че всяка равнинна 3-свързана графа е графика на изпъкнал полиедър.
Печалби и свързани с тях резултати
Човек може да докаже по-строго твърдение на теоремата на Щайниц, че всеки полиедърен график може да бъде реализиран като изпъкнал многостен с върхове с цели координати. Целите числа, получени в оригиналното доказателство на Щайниц, са двойно експоненциална функция [en] от броя на върховете на дадения полиедър. Следователно записването на тези числа изисква експоненциален брой битове [12] . Въпреки това последващи изследвания откриха алгоритъм за визуализация на графика, който изисква само O(n) бита за всеки връх [13] [14] . Можете да облекчите изискването всички координати да са цели числа и да зададете координати по такъв начин, чеx-координатите на върховете да са различни цели числа винтервал [0,2n− 4], а другите две координати ще бъдат реални числа от интервала [0,1], така че всяко ребро да има дължина поне една, докато обемът на полиедъра ще бъде ограничен до O(n) [15] .
Във всеки политоп, който представлява даден полиедърен графG, лицата наGса точно цикли вG, които не разделятGна два компонента. Тоест, премахването на цикъла, съответстващ на лице отG, дава свързан подграфG. Можете предварително да укажете формата на което и да е лице на полиедъра - ако изберете цикълC, който не разделя графиката на части и подредите върховете му под формата на двумерен изпъкнал многоъгълникP, тогава има многостенно представянеG, в което лицето, съответстващо наC, е равно наP[16] . Също така винаги е възможно даден полиедрален графGи произволен цикълCда намерят реализация, в коятоCобразува силует на реализация при паралелна проекция [17] .
Теоремата за опаковане на кръгове на Кьобе-Андреев-Търстън може да се разглежда като друго укрепване на теоремата на Щайниц, че всеки 3-свързан планарен график може да бъде представен като изпъкнал полиедър по такъв начин, че всичките му ръбове да докосват една и съща единична сфера [en] [18] . По-общо казано, акоGе многостенна графа иKе гладко триизмерно изпъкнало тяло, може да се намери многостенно представянеG, в което всички ръбове докосватK[19] .