Гъвкав полиедър
Гъвкавият полиедъре многостен (по-точно полиедърна повърхност), чиято пространствена форма може да се променя чрез непрекъсната деформация във времето, при което всяко лице не променя размера си (т.е. движи се като твърдо тяло), а деформацията се извършва само поради непрекъсната промяна на двустенните ъгли. Такава деформация се наричанепрекъснато огъванена полиедъра.
Съдържание
Има много красиви и нетривиални твърдения в теорията на гъвкавите полиедри. Следват най-важните факти, установени до момента, в хронологичен ред:
- Нито един изпъкнал многостен не може да бъде гъвкав. Това непосредствено следва от теоремата на Коши за уникалната определеност на изпъкнал многостен, доказана през 1813 г.
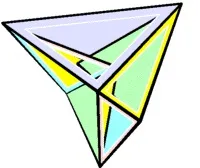
- Първите примери за гъвкави полиедри са построени от белгийския инженер и математик Раул Брикар през 1897 г.[1]. Сега те се наричат октаедри на Брикар. Те не само не са изпъкнали, но и имат самопресичания, което прави невъзможно построяването на подвижния им картонен модел.
- През 1976 г. американският математик Робърт Конъли за първи път конструира гъвкав полиедър без самопресичания [2] .
- От всички известни понастоящем гъвкави полиедри без самопресичане, най-малък брой върхове (девет) има полиедър, конструиран от немския математик Клаус Щефен [de][3] .
- Има примери за гъвкави полиедри, които са реализации на тор [4] или бутилка на Клайн, или като цяло двумерна повърхност от всеки топологичен род.
- От формулата на Schläfli следва, че всеки гъвкав полиедър в процеса на огъване запазва така наречената интегрална среднакривина, тоест число, равно на ∑ ℓ ( π − α ( ℓ ) ), където ℓ е дължината на ръба ℓ , α ( ℓ ) е стойността на вътрешния двустенен ъгъл при ръба ℓ , а сумата се простира до всички ръбове на многостена [5] .
- Теорема на Сабитов[6] : всеки огъващ се многостен запазва обема си по време на огъване, т.е. той ще се огъне дори ако е пълен с несвиваема течност.
- През 2012 г. А. Гайфулин доказва многомерен аналог на теоремата на Сабитов — всеки гъвкав многостен с размерност n ≥ 4 запазва обема си при огъване. [7]