Интересно за космологията
Три модела на Александър Фридман
Известните гравитационни уравнения на Айнщайн са система от десет частични диференциални уравнения. Грубо казано, те показват как разпределението на масите в пространството влияе върху кривината на това пространство. С други думи, те показват как метриката на пространството зависи от разпределението и движението на масите и как на свой ред същата метрика определя движението на материята.
Поради чисто математически трудности системата от уравнения на Айнщайн не се поддаваше на общо решение. Трябваше да отида до различни опростявания.
Тези, които са учили и работили заедно с Фридман, често си спомнят любимата му поговорка: „Не е ли възможно да изхвърлите нещо тук?“ Не е ли от тези позиции той подходи към решаването на уравненията на Айнщайн? Той обаче не отхвърли ламбда члена на системата на Айнщайн, той просто реши уравненията. Оказва се, че са възможни много решения. Случаят с λ=0 е особено интересен. Това решение е толкова интересно, че си струва да се спрем на него по-подробно.
В първата си работа А. Фридман запазва всички предположения на Айнщайн, с изключение на стационарността, и изучава получените нестационарни хомогенни изотропни модели със затворено пространство с постоянна положителна кривина. В същото време, за разлика от Айнщайн, той успя да получи нетривиални решения на уравнения без космологичния член. Какви са теоретичните модели, получени от петроградския математик?
Първо, те бяха нестационарни. Радиусът на кривината и плътността на материята във Вселената са се променили с времето. И съдбата на модела на света зависи от това каква стойност да изберете средната плътност.
Представете си ρ=ρcr: средната плътност е равна на някаква определена критична стойност.Може да се изчисли по проста формула, като се използват стойностите на някои "световни константи". Но сега не ни трябва. Достатъчно е, че такава стойност съществува. При критичната плътност на материята пространствената част на четириизмерния свят е плоска. Това обаче не е неподвижният модел на света на Минковски, който вече обсъдихме. Решението на Фридман направи вселената подвижна! Всички разстояния в космоса растат, т.е. частиците се разлитат в различни посоки със скорост, която за малки разстояния е приблизително пропорционална на самото разстояние.
Ако за по-голяма яснота едно измерение бъде изоставено и преминем към двуизмерно пространство, което се променя във времето, тогава такъв модел може да си представим като гумен филм, равномерно опънат в различни посоки. Полепналите по повърхността й прашинки ще играят ролята на звездни системи – галактики.
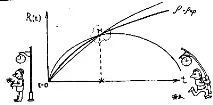
Вижте нашата рисунка. Той показва графика на промените на разстоянието в такъв модел. Сухата абстрактна крива всъщност съдържа цял приключенски роман, само в криптирана форма.
Нека започнем декодирането от най-лявата точка на нашата графика. Тя убедително казва, че някога всички разстояния между всякакви две точки във Вселената са били незначителни. Нямаше пространство, нямаше време, нямаше звезди, нямаше планети, нямаше мъглявини. Нищо. Това е зоната на нулево време. Тогава заработи определен механизъм и материята започна да се появява, частиците й започнаха да се разлитат, започна обратното броене на времето, пространството започна да се разширява - разстоянията между всеки две частици материя започнаха да растат със скорост, пропорционална на самото разстояние. Това означава, че далечните частици се движат с по-висока скорост, докато по-близките се движат с по-ниска скорост.
Застречинг фолио, такова твърдение не подлежи на съмнение. Маркирайте една от прашинките на нейната повърхност и си представете, че сте наблюдателят. С увеличаването на повърхността на филма най-близката до вас прашинка ще се отдалечи от вас с някаква много определена скорост.
По-отдалеченото ще ви се стори много по-пъргаво. Неговата скорост ще бъде по-голяма от най-близката и т.н.
По-късно това решение е използвано от Айнщайн и де Ситер. И затова понякога този най-прост модел се нарича името на тези учени.
Но статията на Фридман съдържа по-„трагично“ решение. Той предположи, че средната плътност на материята във Вселената е по-голяма от критичната. На първо място, това изисква отхвърляне на евклидовото пространство и преход към сферично, риманово триизмерно пространство и дори с променлив радиус на кривина.
В същото време началото, т.е. прословутата „нулева точка“, не се различаваше от началото на предишния модел.
Но тогава всичко се обърка. Радиусът на неевклидово сферично пространство, както можете да видите от следващата фигура, не се увеличава безкрайно. В точка М той достига максимум и след това отново намалява до нула. Това означаваше, че ще дойде момент в историята на разширяващата се Вселена, когато „отстъплението“ ще спре, след което всичко ще тръгне в обратната посока. Компресията ще започне. И след известно време планетите, звездите и галактиките отново ще се слеят в единна бучка праматерия. Този модел се нарича затворен.
През 1924 г. А. Фридман публикува нова работа върху теорията на Айнщайн. Наричаше се „За възможността за свят с постоянна отрицателна кривина“. В новата си работа той изследва уравненията на Айнщайн, като приема, че плътността на материята във Вселената е по-малка от критичната. Нов модел с неевклидовгеометрия - безкрайно разширяващо се пространство с отрицателна кривина. Хиперболичното пространство на Лобачевски, което предизвика толкова много подигравки по време на живота на Великия геометър, получи правото да съществува наравно с Евклидовото и Римановото. Радиусът на пространството на Лобачевски нараства малко по-бързо, отколкото в първия модел. За да покажем това, ние се опитахме да изправим кривата на третата графика, която виждате на предишната страница.
Това са трите модела на Вселената на Фридман. Всички те започват с нулев радиус. Всичко се разширява. Две от тях твърдят ненулевата кривина на пространството.
Но как да повярваме на тези теоретични аргументи? Как да се уверим, че вселената, която човечеството от незапомнени времена вижда като една и съща, всъщност е в състояние на непрекъснато движение, разширяване, разпръскване. Как да разберем, че дори в далечното минало, но имаше такъв момент, когато целият свят беше компресиран в една точка? Моментът на началото на всичко, дори и нашето време. Как в крайна сметка да се уверим, че пространството около нас има кривина? И кой от трите модела на Фридман трябва да се приеме за най-близък до обективната реалност?
