ИЗЧИСЛЯВАНЕ И МОДЕЛИРАНЕ НА МАГНИТНИ ПОЛЕТА, СЪЗДАДЕНИ ОТ СИСТЕМАТА "ПРЪСТЕН НА ХЕЛМХОЛЦ - СОЛЕНОИД" -
Изчисленията и моделирането на магнитни полета за системата "пръстен на Хелмхолц - соленоид" са извършени по време на проектирането и създаването на комплекс за тестване на инклинометрови магнитометри. Този комплекс [1, 4] дава възможност да се проверяват магнитометрите на инклинометъра директно на местата за сондиране на нефтени и газови находища.
Целта на работата е да потвърди възможността за създаване на еднородно магнитно поле с определена стойност в обем, ограничен от геометричните размери на инсталацията.
Общият изглед на комплекса е показан на фиг. 1.
Комплексът се състои от инсталация 1 за базиране върху нея на тествания инклинометър 5, комуникационен блок 2 с компютър 3, свързващи кабели и източник на захранване на инсталацията 4. За работа с комплекса е подходящ всеки персонален компютър. Системата "пръстен на Хелмхолц - соленоид" се използва за създаване на постоянно насочено магнитно поле с известна величина, с помощта на което се проверяват инклинометърните магнитометри.
Изчисляване на пръстени на Хелмхолц
Пръстените на Хелмхолц се наричат система от две еднакви тънки намотки, разположени коаксиално на разстояние, равно на техния радиус. В пространството между намотките се получава силно равномерно поле [2].
Общият модул на магнитното поле може да се получи от закона на Био-Савар-Лаплас:
(1)
където µ0 = 1,257 · 10 –6 H/m; I - ток, протичащ през завоите на намотките на пръстените, в ампери; R е радиусът на намотката, в метри; x е разстоянието по оста на намотките, в метри.
Намотките се състоят от N навивки. Общ ток N∙I.
За система от два пръстена на Хелмхолц изразът за магнитна индукция в геометричния център приема формата:
(2)
Магнитното поле, създадено от пръстените на Хелмхолц във всяка точка на надлъжната ос X, се изчислява по формулата:
(3)
Магнитометрите на инклинометъра са поставени в цилиндричен корпус с диаметър 30 mm на разстояние 10 mm един от друг и са разположени правоъгълно. Дължината на самия магнитометър е 28 мм. Въз основа на това е необходимо да се създадат пръстени на Хелмхолц и соленоид с такива размери, чието магнитно поле да бъде равномерно в обем два пъти по-голям от обема, зает от чувствителните елементи.
Въз основа на техническите изисквания към продукта пръстените Helmholtz и соленоидът трябва да се захранват от един източник, чийто максимален ток не трябва да надвишава 0,3 A. Максималният диаметър на пръстените е 300 mm. Диаметърът на използвания навиващ проводник е 0,45 mm. Помислете за работната зона, в която грешката на максималното равномерно магнитно поле не надвишава 1%. Такава грешка е приемлива за тестване на работата на инклинометъра магнитометри.
Имайки първоначалните данни, съгласно формулата (2) е възможно да се изчисли броят на завъртанията на намотаващия проводник на всеки пръстен:
(4)
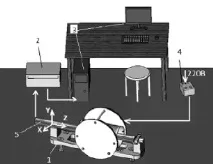
Ориз. 1. Общ изглед на инсталацията
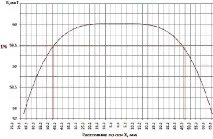
Ориз. 2. Разпространение на магнитното поле в центъра на пръстените на Хелмхолц по оста X
Съпротивление на система от 2 пръстена:
, (5)
където ρ = 0,0178 Ohm mm²/m е съпротивлението на медта; lav = π∙D∙n е дължината на жицата в един пръстен. Ефективното напрежение в краищата на намотаващия проводник на пръстените се определя от:
(6)
Изчислените стойности на индукцията на магнитното поле, създадено от пръстените на Хелмхолц по оста X, са показани на фиг. 2. Зоната на максимално равномерно магнитно поле с грешка от 1% по оста X е 90 mm.
Изчисляване на соленоида
Диаметърът на соленоида трябва да бъде възможно най-голям и да пасва между пръстените на Helmholtz.
Изходни данни: радиус на намотката Rk = 0,145 m; ефективен ток I = 0,3 A;дължина на бобината lk = 0,3 m; диаметър на проводника dp = 0,00045 m; индукция на магнитно поле на соленоид B = 0,000060 T.
Сила на магнитното поле:
(7)
Изразът за изчисляване на силата на магнитното поле на соленоида:
(8)
където B е индукцията на генерираното магнитно поле, T; I - сила на тока, A; n е броят на навивките на единица дължина, n = N/l; R е радиусът на соленоида, m; l е дължината на соленоида, m; x е координатата на точка върху оста на соленоида.
Индукцията на магнитното поле вътре в соленоида [2], в средата на надлъжната ос, т.е. при x = l/2, се изчислява като:
(9)
От формула (9), като имаме известни данни за магнитната индукция, силата на тока и геометричните размери на соленоида, можем да намерим необходимия брой навивки на намотката:
(10)
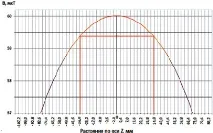
Ориз. 3. Разпространение на магнитното поле в центъра на соленоида по оста Z
Стъпка на навиване на проводника на соленоида:
(единадесет)
където t е стъпката на намотката на проводника, mm.
Съпротивлението на соленоида се определя като
(12)
където dп – диаметър на проводника, m; ρ е съпротивлението на медта 0,0178 Ohm mm²/m; Работното напрежение се определя:
(13)
Изчислените стойности на индукцията на магнитното поле, създадено от соленоида по оста Z, са показани на фиг. 3.
Зоната на максимално равномерно магнитно поле с грешка от 1% по оста Z е 34 mm от центъра на соленоида в различни посоки.
Компютърна симулация на магнитни полета
Моделирането на магнитни полета, създадени от системата "Пръстени на Хелмхолц - соленоид", е извършено в среда "Comsol" [3]. Магнитното поле е изчислено в модула "Магнитни полета (mf)" [5]. Данните за геометричните размери, големината на протичащите токове и броя на завоите бяха използвани същите като при аналитичното изчисление,както и съгласно техническото задание за разработване на комплекс за проверка на магнитометрите на инклинометъра. За по-подробна визуализация на разпространението на силовите линии на магнитното поле в системата "пръстени на Хелмхолц - соленоид" те са представени в опростен вид. Тъй като пръстените на Хелмхолц и соленоидът се включват последователно, първо се моделира работата на соленоида, а след това работата на пръстените на Хелмхолц. На фиг. 4а показва разпространението на линиите на магнитното поле в соленоида.
Показано на фиг. 4b, зависимостта показва, че зоната на максимално равномерно магнитно поле с грешка, не по-голяма от 1%, е 33 mm в двете посоки от центъра на соленоида по оста Z.
На фиг. 5а показва разпространението на линиите на магнитното поле по време на работата на пръстените на Хелмхолц.

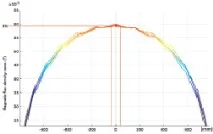
Ориз. 4. а - разпространение на линиите на магнитното поле в соленоида; b - стойността на магнитната индукция на соленоида в зависимост от координатата на точката, разположена на надлъжната ос Z
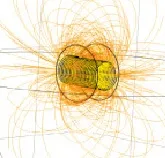
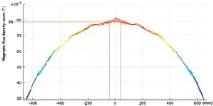
Ориз. 5. а - разпространение на линиите на магнитното поле в пръстените на Хелмхолц; b - стойността на магнитната индукция на пръстените на Хелмхолц, в зависимост от координатата на точката, разположена на надлъжната ос X
Показано на фиг. 5б, зависимостта показва, че зоната на максималното равномерно магнитно поле с грешка, която не надвишава 1%, е 40 mm в двете посоки от центъра на пръстените на Хелмхолц по оста X.
Заключение
Резултатите от аналитичното моделиране показват несъответствия с графиките на зависимостта на големината на магнитното поле от координатата на точка по осите на соленоида и пръстените на Хелмхолц, получени чрез моделиране в среда Comsol. Несъответствието между резултатите от симулацията в средата Comsol и изчислените стойности за регионите на пространството, където магнитното полеравномерно, не надвишава 3% за соленоида и 12% за пръстените на Хелмхолц. Това се дължи на факта, че при използване на намотки от пръстени на Хелмхолц с голям брой навивки, втората производна, когато се разшири в серия на Тейлър, не е равна на нула за двойки навивки, разположени на разстояние, различно от R/2 по оста X спрямо геометричния център на системата. В резултат на това се увеличава нееднородността на магнитното поле. Изчисленията и моделирането на магнитни полета за системата "пръстен на Хелмхолц - соленоид" при зададени геометрични размери и електрически параметри на захранването на системата показват, че когато магнитометрите на изпитвания инклинометър са разположени в центъра на системата, е възможно да се проверят магнитометрите на инклинометъра в полето.
Рецензенти:
Дмитриев V.S., доктор на техническите науки, професор, Национален изследователски Томски политехнически университет, Томск;
Бориков V.N., доктор на техническите науки, директор на Института за безразрушителен контрол, Национален изследователски Томски политехнически университет, Томск.