Изчисляване на ефективността на инвестиционен портфейл в Excel
Както беше обещано в предишната статия, тази ще ви каже как да изчислите основните показатели за ефективност на инвестиционен портфейл директно в Excel http://utmagazine.ru/posts/5908-kak-rasschitat-effektivnost-portfelya-cennyh-bumag
Вече разбрахме, че въпреки привидно сложните термини и показатели, всъщност не е толкова трудно да се изчислят тези показатели. В случай на изчисления в Excel, тези изчисления ще бъдат още по-лесни за извършване, тъй като процесът като цяло е автоматизиран. Необходимо е само правилно да подредите клетките и да направите връзки към съответните клетки. И тъй като всичко е ясно с показателите за рентабилност като цяло, ще бъдат разгледани само изчисления на рисковите показатели.

Тъй като в предишната статия вече имаше дефиниции на основните рискови индикатори, в този случай, за да не се претоварваме с ненужна информация, ще говорим само за самите изчисления. За всичко по ред.
За всеки случай нека повторим основните рискови индикатори: стандартното отклонение на доходността на портфейла и на всеки актив поотделно от пазарната доходност; Коефициент на Шарп; бета коефициент; коефициент на Трейнор; Алфа Йенсен; коефициент на Швагер; коефициент на Сортино; М-квадрат. Нека да разгледаме изчислението на всеки от тези показатели в Excel един по един. Вероятно си струва да успокоим всички - това е доста лесно да се направи, поне много по-лесно, отколкото може да изглежда на пръв поглед. Освен това, в случай на изчисления в Excel, е достатъчно просто да използвате съответните функции. Незабавно направете резервация, че всички цифри са условни и са взети от предишната статия.
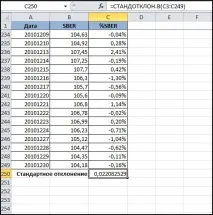
Стандартното отклонение е най-лесният за изчисляване от всички показатели. За изчисляването му е необходим само добивът.портфолио спрямо пазара. Необходимо е само да вмъкнете формулата "STDEV.B (...)" в съответната клетка и да изберете подходящия масив с данни за добива.
Коефициентът на Шарп е разликата в възвръщаемостта на портфейл към безрисков актив, разделена на стандартното отклонение на портфейла. Формулата е лесна за изчисляване: с възвръщаемост на портфейла от 2% и полученото стандартно отклонение от 0,5%, както и възвръщаемост на безрискови активи от 0,4%, трябва да извадите втората клетка от първата клетка и да разделите всичко това на третата.
Бета коефициентът е скоростта на промяна на възвръщаемостта на портфейла в сравнение с пазарната възвръщаемост. Съответно е необходимо да се изчисли математически колко възвръщаемостта на пазара влияе върху възвръщаемостта на портфейла. Формулата използва само два показателя: портфолио и пазарна ковариация (произведението на сумите на корелация и стандартното отклонение на портфейла и пазара) и дисперсията на пазарната възвръщаемост (изчислена като стандартното отклонение на квадрат).
Първо, нека изчислим коефициента на ковариация. При корелация между портфейла и пазара от 0,7, пазарно стандартно отклонение от 0,3% и стандартно отклонение на портфейла от 0,5%, ковариацията е 0,7*0,3%*0,5%=0,0000105. За да се изчисли пазарната дисперсия, е достатъчно да се повдигне на квадрат стандартното отклонение: 0,3%^2=0,000009. От тук намираме бета коефициента 0,0000105/0,000009=1,16667.
От получените данни сега изчисляваме коефициента на Трейнър - съотношението на премията за пазарен риск и самия риск на портфейла. За изчисляването му са необходими само три показателя: обща пазарна възвръщаемост, обща възвръщаемост на портфейла и бета на портфейла. С получените по-горе показатели се оказва: (20% -15%) / 1,16667 \u003d 0,04285.

Алфата на Jensen е съотношение, което показва колко по-ефективно е активното управление на портфейла в сравнение с пасивното.За изчисляване са необходими 4 показателя: средна възвръщаемост на портфейла (2%), средна пазарна възвръщаемост (1,5%), възвращаемост на безрискови активи (0,4%) и бета коефициент на портфейла (1,16667). Колкото по-висока е стойността на този коефициент, толкова по-ефективно се управлява портфейлът.

Коефициентът на Швагер е съотношението на печалбата от портфейла към средното максимално усвояване. Условно взехме данни за една година с портфолио от $500 000. За изчислението са необходими само два показателя: средната годишна възвръщаемост на портфейла (500 * 0,2 = 100 хиляди долара) и максималното усвояване (нека условно вземем 5%: 500 * 0,2 = 25 хиляди долара). След това правим изчислението по формулата.
Коефициентът на Сортино, както и коефициентът на Шарп, показва ефективността на управлението на портфейла, но не по-ниска от минималната допустима възвръщаемост. Първо, нека изчислим минималната допустима възвръщаемост. По правило за такъв показател се приема възвръщаемостта на безрисков актив (0,4%). Така, като се вземе предвид броят на работните дни в годината (условно 280), минималната допустима дневна доходност е 0,4%/280=0,0014%.

Освен това е необходим брой дни под минимално допустимата доходност (условно ще приемем този показател като 15). След това може директно да се изчисли самият коефициент на Сортино. Изчислено, както следва: (2%-0,0014%)/15=0,0013.

И накрая, последният коефициент е М-квадрат или просто М 2 . Този индикатор показва колко по-висока възвръщаемост показва едно портфолио в сравнение с безрисков актив. За изчислението са необходими четири показателя: средната възвръщаемост на портфейла (2%) и безрисковия актив (0,0014%), стандартното отклонение на възвръщаемостта на портфейла (условно ще приемем 1%) и стандартното отклонение на пазарната възвръщаемост (условно ще приемем 0,5%).
Това е всичко.Изчисляването на всички тези коефициенти в Excel се оказа не толкова трудно, както беше обещано в началото на статията. След усвояването на тези два материала се надяваме, че ключовите елементи на портфолио анализа са усвоени успешно.