Изчисляване на сложни вериги с помощта на правилата на Кирхоф (общ метод на изчисление)
ITNIT IB
РАБОТА ПО ЕЛЕКТРОТЕХНИКА #1
ИЗЧИСЛЯВАНЕ НА ПРАВОТОКОВИ ВЕРИГИ
Основни понятия
Подреденото движение на заредени частици се наричаелектрически ток. Обичайно е да се характеризира сток- скаларна стойност, равна на заряда, преминаващ през напречното сечение на проводника за единица време. Ако през времетоdtпремине зарядdq, тогава токътIпо дефиниция е равен на:
| (1) |
Единицата за сила на тока е ампер.
За да се получи ток във всеки проводник в неговите краища, е необходимо да се създаде и поддържа потенциална разлика. Тъй като зарядите се движат под въздействието на електростатично поле, така че потенциалната разлика намалява, са необходими устройства, в които сили, различни от силите на електростатичното поле, биха действали върху зарядите. Такива сили се наричат външни сили. Всички устройства, в които възникват външни сили, се наричат източници на ток(например галванични клетки и др.). Външните сили могат да бъдат причинени от химични процеси, дифузия на носители на заряд в нехомогенна среда, електрически (непотенциални) полета.
Външните сили могат да се характеризират с работата, която извършват върху зарядите, движещи се по веригата. Стойността, равна на работата на външните сили, отнесени към единица положителен заряд, се наричаелектродвижеща сила(ЕМС)ε, действаща във веригата или в нейната секция. Следователно, ако работата на външните сили върху заряда q е равна на A, тогава по дефиниция:
| (2) |
Размерността на ЕМП съвпада с размерността на потенциала.
Електрическа веригае набор от източници на ток, свързващи проводници,устройства или други устройства (активни и реактивни съпротивления). Тази статия обсъжда методи за изчисляване на сложни разклонени вериги, съдържащи източници на ЕМП, свързващи проводници и резистори (съпротивления).Да се изчислитакава верига означава да се намерят стойностите на токовете през всички резистори, като се знаят стойностите на резисторите и стойностите на всички ЕМП, както и (понякога) някои напрежения и мощности. За изчисляване на постоянни вериги се използват законът на Ом и правилата на Кирхоф.
Закони на DC
Закон на Ом за участък от верига
Георг Ом експериментално установява закона, според който силата на тока, протичащ през проводник, в който не действат външни сили, е правопропорционална на напрежението в краищата на проводника.
| I = σU | (3) |
Стойността σ - коефициент на пропорционалност - се наричапроводимостна проводника, реципрочната стойност на проводимостта се наричасъпротивлениена проводника:
| R = 1/σ | (4) |
Размерът на съпротивлението е [ Ohm ], съгласно (3) и (4) [Ohm] = [V/A]. Размерът на проводимостта е [Siemens].
Закон на Ом за електрическа верига (за пълна верига)
Напрежението U в краищата на участъка от веригата, съдържащ източника на ЕМП със стойност E и резистора със съпротивление R, през който протича токътI,е равно на алгебричната сума на E иI∙R, като трябва да се вземе предвид и вътрешното съпротивление на източника на ЕМП.
Правилата на Кирхоф
В практиката често се срещат разклонени вериги, т.е. вериги, състоящи се от няколко устройства, устройства или съпротивления, свързани паралелно, последователно. Изчисляването на такива вериги е значително опростено, ако използваме правилата, формулирани от Кирхоф. Първоправилото се прилага за верижни възли.Възел във веригае точка, където са свързани повече от два проводника.Първото правило на Кирхофгласи, че алгебричната сума на токовете във възел е нула:
| (5) |
Нека сега отделим някои затворени вериги в разклонената верига.
Законът на Ом може да се приложи към отделни участъци от тази верига за участък от веригата.
Може да се покаже, че за всеки затворен участък от веригата уравнението е вярно:
| (6) |
което изразявавторото правило на Кирхоф: за всяка затворена верига сумата от всички падове на напрежение е равна на сумата от всички електродвижещи сили в тази верига. Уравнение (6) е валидно за всички затворени вериги, които могат да бъдат идентифицирани мислено в дадена разклонена верига.
Методи за изчисляване на вериги
Проектиране на сложни схеми с помощта на правилата на Кирхоф (общ метод на изчисление)
Разгледайте веригата на фигура 1:
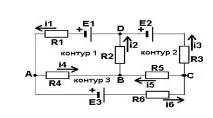
Нека задачата е да се определят посоките и стойностите на всички токове през резисторите, въз основа на зададените стойности на ЕМП (E със съответното число) и съпротивленията на резисторите. За посока на тока приемаме посоката на движение на условните положителни заряди. (в този случай те казват, че токът тече от "плюс" към "минус". Броят на неизвестните токове е 6, така че трябва да направите 6 независими уравнения, свързващи стойностите на тези токове, като използвате правилата на Кирхоф. При съставянето на уравненията се вземат предвид посоките на токовете в клоновете на веригата и тъй като токовете са неизвестни, тези посоки са предварително избрани произволно, така че за всеки от възлите влизат някои токове то и някои изход (по посока на стрелките на диаграмата).Правилото на Кирхоф, токовете, идващи към възела и излизащи от него, трябва да се приемат с различни знаци. В нашия случай ще вземем токовете, идващи към възлите с положителен знак, и токовете, напускащи възела с отрицателен знак. При съставяне на уравнения съгласно второто правило на Кирхоф, ЕМП и токовете, чиито посоки съвпадат с произволно избрана посока на заобикаляне на веригата, обикновено се вземат с положителен знак, останалите - с отрицателен знак.
За възли A, B и C съставяме уравнения според първото правило на Кирхоф:
За последния възел D, избран в диаграмата, ние не съставяме уравнения, защото той няма да бъде независим, тъй като може да бъде получен чрез сумиране на уравненията за възлите, разгледани по-рано. В общия случай за сложна верига, съдържаща N възли, има не повече от N - 1 уравнения според първото правило на Кирхоф. Липсващите уравнения (в нашия случай три) се съставят съгласно второто правило на Кирхоф за независими вериги, произволно избрани във веригата (в резултат на което уравненията също ще бъдат независими). Контурите се считат за независими, ако всеки от тях има поне едно разклонение, което не принадлежи на други контури. За нашата схема избираме трите контура, посочени на фигурата, и се съгласяваме, че посоката на техния обход се счита за посоката на часовниковата стрелка. Според второто правило на Кирхоф имаме:
Решавайки получената система от 6 уравнения, използвайки методи, известни от алгебрата (обикновено чрез метода на детерминантите и матриците), намираме всички неизвестни токове. Ако изчислената стойност на който и да е ток се окаже отрицателна, това означава, че действителната посока на тока е противоположна на произволно избраната. След като определите токовете във веригите, можете, ако е необходимо, да изчислите напреженията и мощностите във веригата. Разгледаният метод е ясен и ви позволява незабавно да определитетекущи стойности, но за сложни схеми отнема много време, тъй като се изисква да се решават системи от голям брой уравнения. Следователно в някои случаи се използват други методи за изчисление. Нека разгледаме някои от тях.