Куб на сбора и куб на разликата
За всякакви стойности на a и b равенството е вярно
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . (1)
( a + b ) 3 = ( a + b ) ( a 2 + 2 a b + b 2 ) = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b 2 + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
Тъй като равенството (1) е вярно за всякакви стойности на a и b, то е идентичност. Това тъждество се нарича сума куб формула. Ако в тази формула вместо a и b заместим някои изрази, например 5 y 3 и 2 z , тогава отново получаваме идентичност.
(5 y 3 + 2 z) 3 = 125 y 9 + 150 y 6 z + 60 y 3 z 2 + 8 z 3. (2)
Следователно формулата на сумата на куба се чете така:
кубът на сбора от два израза е равен на куба на първия израз плюс три пъти произведението на квадрата на първия израз и втория, плюс три пъти произведението на първия израз и квадрата на втория, плюс куба на втория израз.
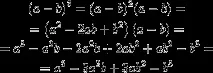
За всякакви стойности на a и b равенството е вярно
( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 . (3)
( a − b ) 3 = ( a − b ) ( a 2 − 2 a b + b 2 ) = a 3 − 2 a 2 b + a b 2 − a 2 b + 2 a b 2 − b 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3
Тъй като равенството (3) е вярно за всякакви стойности на a и b, то е идентичност. Тази идентичност се нарича формула на куба на разликата. Ако в тази формула вместо a и b заместим някои изрази, например 5 y 3 и 2 z , тогава отново получаваме идентичност.
( 5 y 3 − 2 z ) 3 = 125 y 9 − 150 y 6 z + 60 y 3 z 2 − 8 z 3 . (4)
Следователно формулата на куба на разликата гласи следното:
кубът на разликата на два израза е равен на куба на първия израз минус три пъти произведението на квадрата на първия израз и втория, плюс три пъти произведението на първия израз и квадрата на втория, минус куба на втория израз.