КВАДРАТ ПЕТЦИФРЕНИ ЧИСЛА - магия на числата
Овладяването на задачите за умножение 3 по 2 изисква много повече практика, но след като се запознаете с тях, можете да преминете направо към проблемите с 5-цифрено повдигане на квадрат, защото те са сведени до умножение 3 по 2 плюс 2- и 3-цифрено повдигане на квадрат. Например, за да поставите на квадрат числото 46 792, можете да направите следното:
Използвайки закона за разпределение, разделяме проблема на следните операции:
46 000 x 46 000 + 2 (46 000) (792) + 792 x 792.
Последният израз трябва да бъде малко опростен:
46 2 x 1 милион + (46)(792)(2000) + 792 2 .
Но аз не решавам тези задачи в последователен ред, а започвам от средата, защото задача 3 по 2 е по-трудна от повдигането на квадрат на дву- и трицифрени числа.
И така, в съответствие с принципа „първо махнете трудното от пътя си“, изчислявам 792 x 46 x 2 и добавям три нули към края на резултата, тоест ще направя следното:
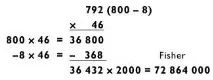
Използвайки метода на изваждане, както е показано по-горе, изчисляваме 792 x 46 = 36 432, след което удвояваме резултата, за да получим 72 864. Прилагането на фонетичния код към числото 864 позволява то да бъде съхранено в паметта като 72 Fisher.
Следваща стъпка: изчисляваме 46 2 x 1 000 000, което е 2 116 000 000.
На този етап можете да кажете: "Два милиарда ...".
Активирайки 72 Fisher в паметта, добавяме 116 милиона към това число, за да получим 188 милиона. Но преди да изразите броя на милионите, трябва да проверите дали единицата трябва да бъде преместена към най-значимата цифра при добавяне на Фишер, тоест числата 864 и 792 2 . Тук всъщност не е нужно да изчислявате 792 2 ; достатъчно е да се определи, че резултатът от изчислението 792 2 ще бъде доста голям, за даобщо от 864 000 до надхвърляне на 1 милион. (Можете да приемете това въз основа на факта, че 800 2 = 640 000 и това число, плюс 864 000, очевидно ще надхвърли 1 милион.) И така, добавете едно към 188 и кажете: "... 189 милиона ...".
Все още имайки предвид думата Фишър, повдигнете на квадрат 792, като използвате метода на 3-цифреното повдигане на квадрат (закръглявайки нагоре и надолу с 8 и т.н.), за да получите 627 264. Накрая добавете 627 към Фишър, тоест 864, и ще получите 1491. Тъй като вече направихме прехвърлянето на единица на мястото на милионите, изхвърлете първото 1 от числото 1491 и кажете: „...4 91 хиляди 264".
Понякога забравям последните три цифри от отговор, защото мозъкът ми е напълно погълнат от големи изчисления. Така че, преди да направя последното събиране, държа числото 2 (от 264) на пръстите си и се опитвам да запомня 64, което обикновено не е трудно да се направи, защото имаме склонност да помним това, което сме чули наскоро. Ако не успея, мога да възстановя последните две цифри, като повдигна на квадрат последните две цифри от оригиналното число, т.е. 92 2 = 8464. Последните две цифри на това число са последните две цифри от 64. (Алтернативно можете да конвертирате числото 264 във фонетичен код.)
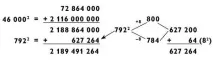
Наясно съм, че процесът на изчисляване на квадрат от 46 792 2 е доста тромав. Представям ви диаграма за това как повдигнах на квадрат това число:
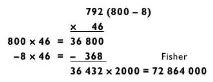
Помислете за друг пример за повдигане на квадрат на петцифрено число: 83 522 2 .
Както преди, изчисляваме отговора в този ред:
83 x 522 x 2000, 83 2 x 1 милион, след това 522 2 .
В първия проблем имайте предвид, че 522 има делител на 9. Така че 522 = 58 x 9. Развивайки 83 като 80 + 3, получаваме:
Резултатът от удвояването на 43 326 е 86 652, което може да се запомни като 86 юлиан. Тъй като 832 = 6889 можем да кажем "Шест милиарда..."
Добавяне 889 + 86 = 975. Преди да кажем „975 милиона“, проверяваме дали сумата от Юлиан (652 000) и квадратът от 522 2 няма да преместят единица на милиарди.
Приблизително оценявайки 522 2 като 270 000 (500 x 540), ние сме убедени, че няма да има пренасяне. Следователно можете спокойно да кажете: "... 975 милиона ...".
И накрая, повдигането на квадрат на 522 по обичайния начин ще доведе до 272 484 и добавянето му към Джулиан (652 000) ще даде последната част от отговора: "...924 484."
Под формата на диаграма решението на този проблем е следното:

УПРАЖНЕНИЕ: КВАДРАТ ПЕТЦИФРЕНИ ЧИСЛА