Лабораторен осцилиращ кръг

Целта на работата:да се изследва честотната характеристика и фазовата характеристика на последователна и паралелна осцилационна верига, да се определи резонансната честота, да се намери коефициентът на качество на последователната верига.

Уреди и материали:осцилационен кръг, осцилоскоп, захранване, генератор, проводници, запас от съпротивления, индуктивности и кондензатори.

Осцилаторната верига е електрическа верига, състояща се от елементи, способни да съхраняват електрическа и магнитна енергия и в които могат да се възбуждат електрически вибрации. Еквивалентната верига на най-простата колебателна верига се състои от капацитет, индуктивност и съпротивление.

Осцилаторните вериги са намерили най-широко приложение в радиоелектрониката като различни честотно-селективни системи, т.е. системи, в които амплитудата на отговора на веригата може да се промени драматично, когато честотата на външното влияние достигне определени стойности, определени от параметрите на веригата. Феноменът на рязко увеличаване на амплитудата на отговора се нарича амплитуден резонанс.

В теорията на веригата обикновено се използва различно определение за резонанс. Под резонанс се разбира такъв режим на работа на електрическа верига, съдържаща капацитет и индуктивност, при която реактивните компоненти на входното съпротивление и проводимост са равни на нула, т.е. няма фазово изместване между напрежението и тока на входа на осцилаторната верига. Такъв резонанс се нарича фазов резонанс. Честотите, съответстващи на фазовия и амплитудния резонанс, като правило са близки и в някои случаи могат да съвпадат.

Най-простата електрическа верига, в която се наблюдава явлението резонанс, е единична осцилаторна верига, състояща се от индуктор и кондензатор, свързани взатворена верига. В зависимост от начина на свързване към осцилаторната верига на източника на енергия се разграничават последователни (фиг. 1) и паралелни (фиг. 2) осцилаторни вериги.

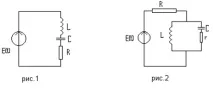Графиката на честотната характеристика за серийна верига е показана на фиг. 3. От графиката може да се види, че графиките на честотната характеристика за C и L се пресичат при резонансната честота w = . Нека намерим честотите, при които честотната характеристика достига максимум. Те са равни

w=(1)

w=(2)

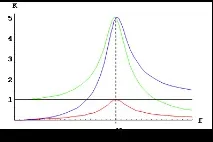
- за R,

- за C,

- за Л.

PFC графиките изглеждат така

фиг.4

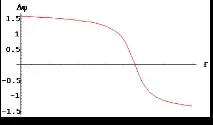
- за Р

Когато се приложи импулсно напрежение, ще получим графика на затихнали трептения (фиг. 5), в аналитичното представяне тази графика има формата

U(t) = Uecoswt(3)

където d е коефициентът на затихване.

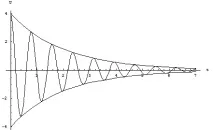
В допълнение към d, системата има друга важна характеристика Q - факторът на качеството, който може да се намери като отношение на U или U към U при резонансната честота. Чрез параметрите на системата изразът за Q може да се запише като

Q = = = (4)

Качественият фактор може да се изрази и чрез d, т.е.

Q = (5)

където T е периодът на трептене.

Задача 1:Изследвайте амплитудно-честотните характеристики на последователен колебателен кръг. Определете добротата. Изграждане на диаграми.

1). За индуктивност(C=10000pF; R=62Ω; L=2.6mH)

Таблица 1:Усилване спрямо честота.

f, kHz	2	5	8	10	13	15	18	20	21	23	25	28	32	35	36	39
К	0,2	1.2	2.7	3.9	4.5	5.1	6.3	8.7	9.9	13	16	20	16	10	6.1	2.1

2). За кондензатор(C=10000pF; R=62Ω; L=2.6mH)

Таблица 2:Усилване спрямо честота.

f, kHz	10	14	16	20	24	26	27	28	тридесет	35	40	50	60	80	100
К	1.2	1.4	1.6	2.5	4.7	8.4	21.7	16.6	7.8	3.4	1.9	0,7	0,6	0,2	0,1

3).За съпротивление(C=10000pF; R=62Ω; L=2.6mH )

Таблица 3:Усилване и фазова разлика спрямо честотата

f, kHz	6	8	9	10	12	14	16	19
К	0,03	0,05	0,06	0,09	0,12	0,14	0,15	0,18
DJ, о	66.6	59.4	55.8	54	52.2	45	43.2	36

f, kHz	25	26	27	28	тридесет	33	35
К	0,57	0,91	0,79	0,66	0,52	0,41	0,28
DJ, о	23.4	10.8	16.2	25.2	109.8	118.8	126

Графика 1. Честотна характеристика за L, C

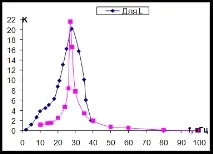
Графика 2. Честотна характеристика за съпротивление

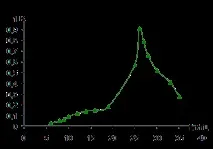
Графика 3. PFC за съпротивление

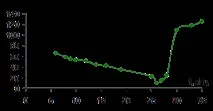
Графика 1 показва, че резонансната честота fp, = 26 kHz.

Определяне на качествения фактор на последователна верига:

(C = 10 000 pF; R = 62 ома; L = 2,6 mH).

Добротата може да се изчисли по два начина:

1-ви начин: използване на параметри на контура:

Получаваме, че Q = 8,14

2-ри метод: според получената честотна характеристика на веригата:

Получаваме, че Q = 13,73

Задача 2:Изследвайте амплитудно-честотната (AFC) и фазово-честотната (PFC) характеристики на паралелна осцилаторна верига. Определете периода на затихване, когато се приложи сигнал от импулсен генератор. Изграждане на диаграми.

Паралелна верига.(C=10000pF; R=1kΩ; L=2,6mH)

Таблица 4:Усилване и фазова разлика спрямо честотата.

f, kHz	1.2	2	3	5	7	10	14	18
К	0,02	0,04	0,07	0,12	0,15	0,20	0,31	0,62
DJ, о	77.4	55.8	54	45	46.8	36	32.4	32.4

f, kHz	23	25	29	тридесет	35	40	50
К	0,95	0,87	0,77	0,64	0,51	0,47	0,33
DJ, о	14.4	21.6	30.6	18	18	18	18

Графиките са показани по-долу

Графика 4. Честотна характеристика на паралелна верига

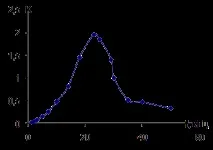
Графика 5. Фазова характеристика за паралелна верига

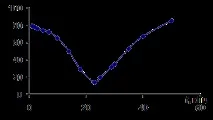
Въз основа на получените данни може да се определи резонансната честота.

Определяне на качествения фактор на паралелна верига:

(C \u003d 10 000 pF; R \u003d 1 kOhm; L = 2,6 mH).

Отново изчисляваме качествения фактор Q по два начина:

= 2,35

1. Изследван е сериен осцилиращ кръг, получени са амплитудно-честотни и фазово-честотни характеристики, определена е резонансна честота, равна на 26 kHz. Несъответствията с теорията са в границите на грешка. Графиките, получени по време на работата, съвпадат с очаквания резултат.

2. Изследван е паралелен колебателен кръг. За него също бяха изградени честотна характеристика и фазова характеристика. Определя се резонансната честотаfp= 23 kHz.

3. Реакцията на последователни и паралелни вериги на импулсно действие беше изследвана и скицирана. Според получената графика е определен периодът на затихване на веригата за тези параметри T = 18*10 -6 s.

4. Въз основа на получените данни бяха определени качествените фактори на последователните и паралелните вериги. Разликите между стойностите на Q са обяснени по-горе.

1. В.Н. Ушаков. „Основи на радиоелектрониката и радиотехническите устройства”. М., "Висше училище", 1976 г.

2. Е.И. Манаев. "Основи на радиоелектрониката". М., "Радио и комуникация", 1985 г.

3. P.N.Urman, M.A. Фадеев: „Изчисляване на грешките в експерименталните резултати“.

---