лабораторна работа - LAB8
5.1. Дискретно-детерминирани модели.
Дискретно-детерминистичните модели представляват друг широк клас динамични системи, работещи в дискретно време. Важно място в моделирането на този клас системи заемат крайните автомати, които представляват системи, които обработват дискретна информация и променят вътрешните си състояния само в допустими времена.
Автоматът е устройство, което приема входни сигнали и приема изходни сигнали, които имат вътрешни състояния, които се променят по време на работата му. Математическите модели под формата на краен автомат се наричат F - схеми от английското finite automate - краен автомат.
Абстрактният краен автомат се характеризира с шест елемента: краен набор X от входове (входна азбука), краен набор Y от изходи (изходна азбука), краен набор Z от вътрешни състояния (вътрешна азбука или азбука на състоянието), преходна функция
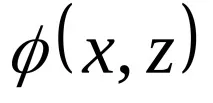
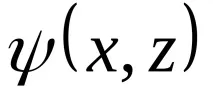
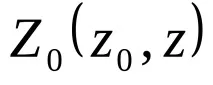
(29)
Такъв автомат функционира в дискретно автоматно време, чиито моменти са цикли - равни времеви интервали, съседни един на друг. Всеки цикъл съответства на постоянни стойности на входни и изходни сигнали и вътрешни състояния x(t), y(t) и z(t), съответно (t = 0, 1, 2, …).
Абстрактният автомат функционира по следния начин: в момента t, намирайки се в състояние z(t), автоматът получава сигнала
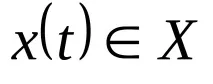
Автоматът в процеса на своята работа осъществява някакво преобразуване на множеството от думи на входната азбука X върху множеството от думи на изходната азбука Y, т.е.ако на входа на краен автомат, зададен в началното състояние
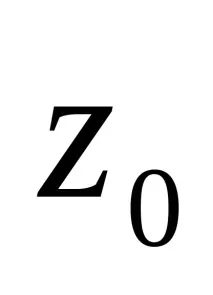
В зависимост от закона на функциониране абстрактните автомати се делят на автомати от първи и втори род.
За F, автомат от първи вид, наречен автомат на Мили, можем да напишем:
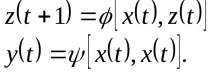
За F, автомат от втори вид, новото състояние и изходният сигнал се определят като:
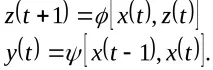
Автомат от втори вид, чийто изходен сигнал се определя от неговото състояние
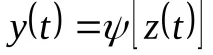
Уравнения (30) - (31), които определят функционирането на F-автомата, са частен случай на уравнение (29) за детерминирана система S с единичен дискретен входен сигнал X.
Според броя на състоянията се разграничават крайни автомати с памет и без памет. Автоматите с памет имат повече от едно състояние, докато автоматите без памет имат само едно състояние. Автоматите без памет се наричат комбинационни или логически схеми. Работата на автомата се описва с уравнението:
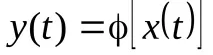
Ако азбуките X и Y се състоят от две букви, тогава функцията се нарича булева.
Според характера на дискретното отчитане на времето крайните автомати се делят на синхронни и асинхронни. В синхронните автомати моментите на постъпване на входните сигнали са строго фиксирани и се определят от синхронизиращи сигнали. След следващия входен сигнал настъпва преход към ново състояние и на изхода се издава сигнал. Отговорът на автомата на всяка стойност на входния сигнал завършва в един цикъл, чиято продължителност се определя от интервала между съседни синхронизиращи сигнали. Асинхроненавтоматът чете входния сигнал непрекъснато за интервал от време, чиято продължителност не е ясно фиксирана. Под действието на входен сигнал автоматът може да променя състоянието си няколко пъти, произвеждайки изходен сигнал за всяко състояние. В този случай автоматът преминава в стабилно състояние, което не може да бъде променено от подаден входен сигнал.
За да се зададе краен F-автомат, е необходимо да се опишат всички елементи на множеството, т.е. неговите азбуки, функции и начално състояние в момент t = 0.
Има няколко начина за задаване на F - автомат, от които най-често използваните са табличен, графичен и матричен.
Табличният начин за описание на абстрактни автомати дефинира преходни и изходни таблици, в които редовете съответстват на входните сигнали X на автомата, а колоните съответстват на неговите състояния Z. В пресечната точка на i-тия ред и k-тата колона на преходната таблица се намира стойността
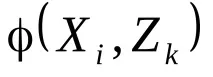
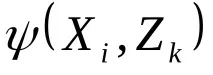
Таблица 5.1.Функции за прескачане.