Лекции Л
МНОГОВАРИАНТЕН СТАТИСТИЧЕСКИ АНАЛИЗ
l Както показва опитът в анализа на масовите източници, броят на обектите може да достигне много десетки и стотици; броят на функциите също може да бъде в десетки. Очевидно директният (визуален) анализ на матрицата с данни с голям брой обекти и характеристики е практически неефективен - можете да идентифицирате само отделни характеристики на изследваната структура, да извлечете илюстративни, конкретни примери.
l В този случай възникват проблемите с уголемяването, концентрацията на първоначалните данни, т.е. конструиране на обобщени характеристики на набор от признаци и набор от обекти. Решаването на тези проблеми може да се извърши с помощта на съвременни методи за многомерен статистически анализ.
l Методи, фокусирани върху анализиране на структурата на набор от признаци и идентифициране на обобщени фактори, са известни като методифакторен анализ, а методите за анализ на структурата на набор от обекти образуват набор от методимногоизмерна класификация.
lМетодите за многомерна класификацияви позволяват да групирате обекти, като вземете предвид всички съществени структурни и типологични характеристики и естеството на разпределението на обектите в дадена система от характеристики.
l Такава класификация се основава на желанието да се съберат в определен смисъл подобни обекти в една група и по такъв начин, че обектите от различни групи да са възможно най-различни.
l Нека всичкиmхарактеристики са количествени. След това всеки отnобектите може да бъде представен от точка вm-измерното пространствено пространство.
l Характерът на разпределението на тези точки в признаковото пространство определя структурата на приликите и разликите на обектите в дадена система от показатели. Приликата на обектите може да се прецени поразстояниетомежду тяхсъответните точки.
l Смисловото значение на това понятие за сходство означава, че обектите са толкова по-близки, сходни, колкото по-малко са разликите между стойностите на едни и същи показатели.
l За определяне на близостта на двойка точки (обектиiиj) в многомерното пространство на количествените признаци се използваЕвклидово разстояние, равно на корен квадратен от сумата на квадратните разлики на стойностите на същите показатели, взети за тази двойка обекти.
l Разстоянието между обектите зависи от „мащаба“ на характеристиките: характеристиките с голям диапазон от стойности играят по-голяма роля при изчисляването на разстоянието между обектите, за разлика от характеристиките с малък диапазон на вариация. Например разстоянията, изразени в километри, ще бъдат хиляда пъти по-малки от тези в метри.
l Поради тази причина данните обикновено сенормализират, т.е. всички характеристики водят до стандартна форма със средна стойност нула и стандартно отклонение единица.
l След нормализиране, обектите по оста на всяка характеристика запазват относителната си позиция, но „мащабът“ на измерване на характеристиката става същият.
l Ако изчислите разстоянията за всички двойки обекти, получавате квадратна таблицаDс размерm´m(матрица на разстоянието); матрицата на разстоянието очевидно есиметрична, тъй като разстоянието от обектiдо обектjе точно същото като разстоянието от обектjдо обектi.
l Матрицата на разстоянието D служи като основа заагломеративно-йерархичния метод, чиято основна идея е последователно да се комбинират групирани обекти - първо най-близките, а след това все по-отдалечените един от друг.
l Процедураизграждането на класификация се състои от последователни стъпки, всяка от които съчетава двете най-близки групи обекти (клъстери). Клъстер (от английскиCluster) е клъстер, „група“, група от обекти, характеризиращи се с общи свойства.
l Има различни начини за определяне на разстоянията между клъстерите (различителни методи за клъстерен анализ). Обикновено близостта на два клъстера се определя като средното разстояние между всички такива двойки обекти, където един обект от двойката принадлежи на един клъстер, а другият принадлежи на друг.
l На първата стъпка от процедурата на агломеративно-йерархичния метод се определя двойка обекти, разстоянието между които е минимално.
l Тези обекти се комбинират в един клъстер, редът и колоната, съответстващи на първия от тези обекти, се зачертават в матрицата и разстоянията от новия клъстер до всички останали клъстери (обекти) се изчисляват като средната стойност на разстоянията от обектите на първия клъстер до всички останали.
l Накрая, тези стойности се въвеждат в реда и колоната на матрицата на разстоянието, съответстваща на втория обект от първия клъстер.
l На втората стъпка от процедурата матрицата на разстоянието, намалена с един ред и една колона, отново определя минималното разстояние и формира нов клъстер. Този клъстер може да бъде изграден чрез комбиниране на два обекта или един обект с клъстера, изграден в първата стъпка.
l Отново един ред и една колона се задраскват в матрицата на разстоянието и един ред и една колона се преизчисляват и т.н.
l Така йерархичният метод на клъстерния анализ включваn– 1 подобни стъпки.
l В този случай след всяка стъпка броят на клъстерите намалява с един и матрицата на разстояниетонамалява с един ред и една колона. В края на тази процедура ще се получи един клъстер, обединяващ всичкиnобекта.
l Резултатите от такава класификация често се изобразяват катодендрограма(дърво с йерархична структура), съдържащоnнива, всяко от които съответства на една от стъпките на описания процес на последователно разширяване на клъстери.
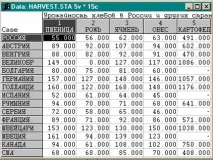
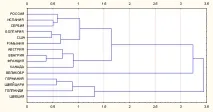
l Анализирайки структурата на получената класификация, може да се види, че страните могат да бъдат разделени на три групи (Германия, Швейцария, Холандия и Швеция); (Австрия, Унгария, Франция и Канада); (България, Испания, Сърбия, България, САЩ, Румъния).
l Третата група обаче се състои от две подгрупи: в едната са България, Испания и Сърбия, а в другата България, САЩ и Румъния.
l В допълнение, втората и третата група на определено ниво образуват общ клъстер, докато първата група остава доста далеч от този клъстер.
l Възниква въпросът защо Великобритания не е включена в нито един от трите клъстера, а заема специална позиция в схемата? Ако внимателно разгледате изходните данни, причината става ясна: съответната колона на изходната таблица има нулева стойност.
l Нека коригираме класификационните параметри, като изключим променливата "ръж" от характеристиките, за които се извършва анализът.
l След това повтаряме процедурата за класифициране и разглеждаме новия резултат.
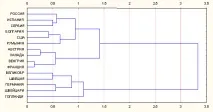
l Друг метод за клъстерен анализ е т.нар.k-означава. За разлика от агломеративно-йерархичния метод, който не изисква предварителна оценка на възможния брой групи от обекти, този метод се основава на хипотезата за най-вероятния брой класове. Задачата на метода в този случайе изграждането на даден брой клъстери, които трябва да се различават максимално един от друг.
l Процедурата за изграждане на клъстери започва с произволно групиране на обекти. Това е последвано от итеративен процес на преместване на обекти между групи, за да се минимизира вътрешнокласовата дисперсия на индикаторите и да се увеличи максимално междукласовата дисперсия (т.е. всеки клъстер трябва да се състои от най-много „сходни“ обекти, а самите клъстери трябва да бъдат толкова „различни“ един спрямо друг).
l Резултатите от този метод ви позволяват да получите центровете на всички класове (и други параметри на описателната статистика) за всяка от оригиналните характеристики, както и да видите графично представяне на това колко и в какви параметри се различават получените класове.
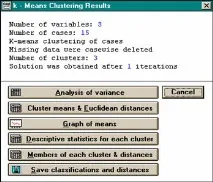
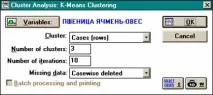
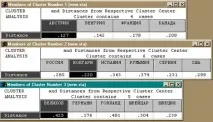

l Сложността, хетерогенността на системите, изучавани от историческата наука, се проявява и във факта, че обекти, принадлежащи към един и същи тип, в различна степен, имат присъщите му свойства. Следователно, когато се разграничават типове (класове) обекти, трябва да се вземе предвид наличието на класядрои неговатапериферия.
lЯдротона даден тип представлява група от обекти, които се характеризират с концентриран израз на всички специфични свойства на типа, които определят качествената разлика на този тип от всички останали.
lFuzzy setе клас от обекти, в който няма рязка граница между тези обекти, които са включени в този клас, и тези, които не са включени в него.
l Принадлежността на всеки обект към размит набор се описва с помощта на стойност, която приема стойности от 0 до 1. Тази стойност се наричастепен на членство; колкото по-близо е до 1, толкова по-голяма е степента на принадлежност на обекта към товаразмит набор.
l Когато се използва TNM (теория на размитите множества), несигурността е свързана с размиване на границите между класовете.
l Концепцията за размиване се отнася до класове, в които може да има различни степени на принадлежност, междинна между пълно членство (1) и нечленство (0) на обекти към класа. В този случай несигурността не е свързана със случайност, тя се запазва дори при наличие на пълна информация за обектите.
lЯдротона размит набор се дефинира като такъв набор от обекти, за всеки от които степента на принадлежност към този размит набор надвишава някаквапрагова стойност(например 0,9).

l Дадените резултати като цяло съответстват на получените по-рано. Ние избираме ядрото на всеки клас според прага за членство, равен на 0,8.
l Първият клас включваше България, България, Испания, Румъния, Сърбия и САЩ. Въпреки това, за разлика от резултатите от "твърдата" класификация, може да се види, че само четири от тези шест държави са включени в ядрото на класа, докато Румъния и Съединените щати принадлежат към неговата периферия, разкривайки известно сходство с обекти от втория клас.
l До известна степен тези страни са преходни обекти от първи към втори клас.
l Вторият клас включваше, както и преди, Австрия, Унгария, Франция и Канада, всички от които принадлежат към ядрото на този клас.
l Тоест вторият клас е по-„сплотен” от първия (същото може да се каже и за третия клас). На фиг. Таблица 6.14 показва, че като цяло 11 държави от 15 са включени в техните класове с тегло на членството от 0,9 до 1, две държави са включени с тегло от 0,8 до 0,9 и две с тегло от 0,7 до 0,8 (Румъния и САЩ).