Лекции Word Част1
Уралски федерален технически университет - UPI Катедра по инженерна графика
ЛЕКЦИИ ПО НАПИСАТЕЛНА ГЕОМЕТРИЯ
Кирилова Татяна Ивановна
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
ИНЖЕНЕРНА ГРАФИКА е общообразователна дисциплина, състояща се от три взаимосвързани раздела: дескриптивна геометрия, инженерна графика, компютърна графика.
ДИСКРИПТИВНА ГЕОМЕТРИЯ – дял от геометрията, който се занимава с
изграждане и изследване на изображения на обекти, разположени в пространството, графични методи.
СИМВОЛИ И СИМВОЛИ
Символи, обозначаващи геометрични фигури и връзки между тях
1. Геометрична фигура - Ф;
2. Точки от пространството - A, B, C, D, L, M, ... 1, 2, 3, 4 ...; Проекции на точки в пространството - A 1, B 2, ... 1 1, 1 2, 1 3;
3. Линии - a, b, c, d, l, m, n ...;
Линиите на нивото са обозначени с −
h - хоризонтална линия; f - фронтална права линия;
w - профилна линия.
Линейни проекции - A 1 B 1, A 2 B 2, A 3 B 3; Използва се и нотацията:
AB - права, минаваща през точки A и B;
I AB I - естествената големина на отсечката или разстоянието от точка А до точка В.
4. Проекционни равнини - P 1, P 2, ... P p;
5. Координатни оси - О X, О Y, О Z където
X – абсцисната ос, Y – ординатната ос, Z – апликативната ос;
6. Равнини - a, b, g, l, m, h ...; проекции на равнини a P 1, b P 2, g P 3 ...;
7. Ъгъл - ABC, w°; b°; g°…;
Ъглова стойност ABC, w - стойност на ъгъл ABC, w
Символи, обозначаващи връзките между геометричните фигури
7. З пресичат се;
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
9. X принадлежи на ;
ОСНОВНИ ЗАДАЧИ НА ДИСКРИПТИВНАТА ГЕОМЕТРИЯ
1. Създаване на плосък геометричен модел на пространствен обект – чертеж или схема). Епюр - в превод от гръцки - чертеж или проект.
2. Решаване на задачи в самолет.
3. Създаване на пространствен обект – разчитане на чертеж (схема).
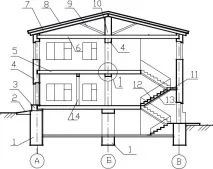
Ориз . 1. Пример за първия проблем на „дескриптивната геометрия“
Чертежът показва чертеж на двуетажна сграда с прозорци, врати,
стълбище. Представената рисунка е плосък модел на пространството
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
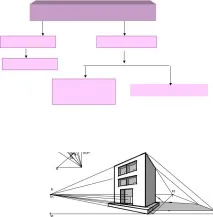
Графичен метод за конструиране на изображения на пространствени обекти е проекцията. В резултат на проектирането се получават проекции на обекти.
Проекцията е процес на получаване на надеждно изображение в чертеж, чрез който е възможно да се представят формата и размерите на обект.
Ортогонални равнинни лъчи Аксонометрични
Ориз . 1. Видове проекция
Проекция - изображение, получено чрез проектиране на обект върху равнина или друга повърхност. Проекцията на обект е набор от проекции на всичките му точки.
Ориз . 2 Централен изглед на сградата. строителна перспектива
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
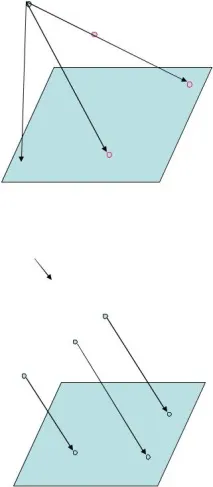
М Б
V p S p
Ориз . 3. Централен проекционен апарат
Ориз . 4. Апарат за паралелна проекция
1. S - проекционен център;
2. P - проекционна равнина;
3. A, B, C - точки от пространството;
4. SA, SB, SC - проектиращи лъчи;
5. Ap , Vp , Sp - проекции на точки върху равнината P .
Перспективни изображения се получават чрез централна проекция
1.с– посока на проекцията ;
2. P - проекционна равнина;
3. A, B, C - точки от пространството;
4. ААп, ВВп, СSp – издадени греди;
5. Ap , Vp , Sp - проекции на точки .
Ако проектиращите лъчи S са перпендикулярни на проекционната равнина -
проекция се нарича - правоъгълна или ортогонална.
Древногръцки се превежда като прав ъгъл. Ако проектиращите лъчи S
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
наклонена към равнината на проекцията под произволен ъгъл, проекцията се нарича наклонена.
Централната и паралелната проекция на една и съща равнина има недостатък:
Невъзможно е недвусмислено да се определи позицията на обект в пространството от една проекция. За недвусмислено определение на обект в пространството Гаспар Монж предложи да се проектира върху три взаимно перпендикулярни равнини.
Образуване на ортогонална система от равнини и координати
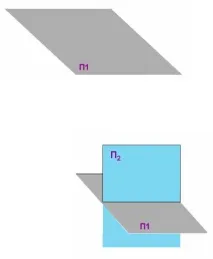
Първата равнина е хоризонтална и се нарича ХОРИЗОНТАЛНА ПРОЕКЦИОННА РАВНИНА. Обозначение на самолета - П 1
Ориз . 5. Хоризонтална проекционна равнина
Втората равнина е разположена вертикално пред наблюдателя и се нарича
- ФРОНТАЛНА РАВНИНА НА ПРОЕКЦИИ. Обозначение на самолета - П 2
Ориз . 6. Хоризонтална и фронтална проекционна равнина
Третата равнина е разположена вертикално вдясно и се нарича - ПРОФИЛНА РАВНИНА НА ПРОЕКЦИИ. Обозначение на самолета - П 3
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
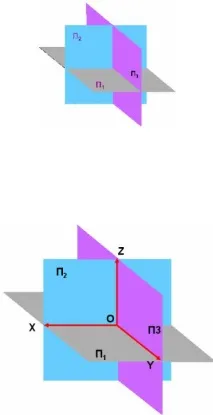
Ориз . 7. Хоризонтална, фронтална и профилна проекционна равнина
Пресичащи проекционните равнини образуват координатните оси: О X – абсцисната ос;
О Y – у-ос;
О Z е оста на приложението.
Пресечната точка на осите O се нарича начало на координатите. Местоположението на точка в пространството се определя от три координати (X, Y, Z).
Ориз . 8. Ортогонална система от равнини и координатни оси
Въведените проекционни равнини разделят пространството на осем октанта: I, II, III, I V, V, V I, V II, V III. В първата четвърт на пространството координатните оси имат положителна посока, следователно в дескриптивната геометрия обектите се намират главно в първата четвърт на пространството.
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
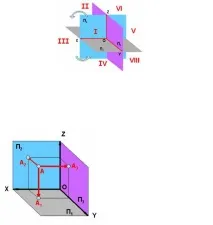
Ориз . 9. Октанти на пространството
Ортографски проекции на точка
Точката е най-простият космически примитив. Нека начертаем проектиращи лъчи, перпендикулярни (ортогонални) на проекционните равнини, докато се пресичат с тях. Пресечни точки на ортогонални, проектиращи лъчи с проекционни равнини - ортогонални проекции на точки.
A 1 - хоризонтална проекция на точка A; А 2 - фронтална проекция на точка А; А 3 - профилна проекция на точка А.
Ориз . 10. Ортогонални проекции на точка
Координатите на точката са разстоянията от точката до проекционната равнина (АА 3 , АА 2 , АА 1 ) или от координатната ос до проекцията на точката (AZ A 2 , A X A 1 , A X A 2 ), както е показано на фиг. 11. Координатите на точката се записват така A (X, Y, Z)
Разстояние АА 3 – координата X на точка А (X A );
Разстояние A A 2 - Y координата на точка A (Y A );
Разстояние A A 1 е Z координатата на точка A (Z A ).
Нека разширим хоризонталната равнина P 1 и профилната равнина P 3, докато съвпадне с фронталната равнина P 2 (виж фиг. 11).
PDF, създаден с пробна версия на pdfFactory Pro www.pdffactory.com
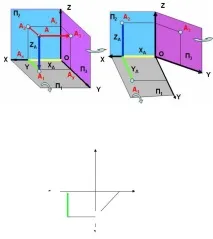
Ориз . 11. Оформянечертеж на ортогонална точка
Фронталната равнина P 2 не променя позицията си. Хоризонталната равнина P 1 е разположена под равнината на предната проекция. Профилната равнина P 3 е разположена вдясно от равнината на предната проекция.