Логаритмични честотни характеристики на динамични връзки
Удобна форма за представяне на честотните характеристики са логаритмичните характеристики, включително логаритмичната амплитудна характеристика (LAH) и логаритмичната фазова характеристика (LPH).
В теорията на автоматичното управление, когато се изучават динамичните свойства на ACS (главно стабилност), се използватлогаритмични честотни характеристики(LFC). Също така, тези характеристики се използват широко при определяне на структурата и параметрите на регулаторите, които формират даден преходен процес в системите за автоматично управление.
Като вземем логаритъм от лявата и дясната страна на уравнението на AFC, можем да напишем
Зависимостите lnA(ω) и φ(ω) са съответно логаритмични амплитудна и фазова характеристики.
За да се оцени съотношението на две хомогенни величини, обичайно е да се използва логаритмичната единица децибел (dB). Връзката между числотоLи числотоAсе изразява с формулатаL= 20 lgA.Например, ако числотоA= 10, тогаваL = 20lgA =20 dB, тъй като lg10 = 1.

LAH и LPH са представени в този случай под формата на графики в правоъгълна координатна система. Абсцисата показва честотата co в логаритмична скала, а ординатата показва амплитудите на LAH в децибели и ъглите на LPH в градуси (или радиани) в единна скала.
Безинерционна връзка. Логаритмирайки AFC на тази връзка, получавамеL(ω)= 20lgk.Тъй катоkне зависи от честотата, LAC на безинерционната връзка ще бъде права линия, успоредна на абсцисната ос (фиг. 9.25).
| Помислете за втория компонент на LAH: |
Апериодична връзка Логаритмирайки AFC на тази връзка, получаваме
От този израз,приемайки, че ω 2T2 2T2>>1, пренебрегвайки единицата, намирамеL2(ω)= - 20 lgωT. Когато ωT =1, радикалният израз ще бъде равен на две иL2(ω)= 3 dB. LAH в този случай може да се представи като две прави линии (асимптоти), спрегнати в точката ωs =1/Т.В този случай честотата ωs се наричаспрягаща;едната от асимптотитеL2(ω)= 0 съвпада с абсцисната ос, а вторатаL2(ω)= - 2 0lgTе наклонен по отношение на нея.
Ъгълът на наклона на втората права линия ще бъде намерен въз основа на следните съображения. При честота ω = ω1, ординатата на правата линия е равна на -20 logω1T,и при честота, например, ω = 2ω1 ще бъде -20lg2ω1T. Намерете разликата между тези ординати:
Така, когато честотата се промени два пъти, правата линия има наклон от -6 dB на октава. Подоктавасе разбира интервалът по абсцисата, съответстващ на двукратна промяна на честотата. Разликата в ординатите с десетократна промяна на честотата ще бъде:
Наклонът на правата линия в този случай е -20 dB на декада (-20 dB/dec.). Поддесетилетиесе разбира интервалът по оста x, съответстващ на десетократна промяна в честотата. Знакът минус показва, че с увеличаване на честотата LAH ординатите намаляват (отрицателен наклон).
 |
На фиг. 9.26 показва спрежението на две асимптоти. Първата е права линия, успоредна на абсцисната ос и отдалечена от нея на 20 lgk.Втората е наклонена спрямо нея с -20 dB/dec. ОбобщавайкиL1иL2, получаваме резултантния LAH на апериодичната връзкаL(ω).В близост до честотата ωc, асимптотите могат да бъдат спрегнати чрез гладка крива, преминаваща през точка, разположена на 3 dB под тяхната пресечна точка. Честотата ωс, при която LAH пресича абсцисната ос, се наричачестотаизрежете.
Логаритмичната фазова характеристика φ(ω) = -arstgωTможе да бъде построена точка по точка. Неговите характерни точки: φ(0) = 0; φ(ωs) = -45°; φ(∞) = -90°.
Оцилаторна връзка. За да се конструира LAX на осцилаторна връзка, препоръчително е да се представи нейното уравнение във формата
 |
Като вземем логаритъм на този израз, получаваме уравненията на логаритмичните амплитудни и фазови характеристики:
Семейството от криви LAH и AFC за една и съща стойност на ω0 и различни стойности на t, конструирани съгласно тези уравнения, е показано на фиг. 9.27. Тези криви са конструирани без да се вземат предвид първият и вторият член на уравнението заLω, тъй като те са константи. За разлика от предишните графики, за да направят кривите универсални, стойностите на ω/ω0 са нанесени по оста x.
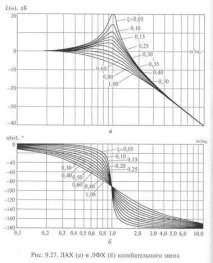
За стойности на ξ от 0,35 до 0,75, с достатъчна точност, вместо APC криви могат да се използват две директни асимптоти, конюгиращи в точката ω/ω0 = 1. Наистина,
Наклонът на втората асимптота, даден от уравнението -20lgω 2, е 12 dB на октава, или -40 dB/dec. За всякакви други стойности%, характеристикитеL(ω) трябва да бъдат построени по точки.
Диференцираща връзка. Като вземем логаритъм на уравнението на тази връзка, намираме
LAHL(ω) е изграден от три компонента (фиг. 9.28). Първият компонент е права линия, успоредна на оста x; вторият компонентL2(ω) = 20lgωTе права линия с положителен наклон от 20 dB/dec и минаваща през точка на оста x, съответстваща на ъгловата честота ωs = 1/T.
Третият компонент има две асимптоти
вие, чифтосване в точката ωs \u003d 1 / T, едната от които съвпада с абсцисната ос, ивторият има отрицателен наклон от -20 dB/dec.
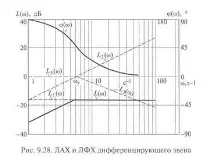

Обобщавайки тези три компонента, получаваме резултантния LAH на диференциращата връзкаL(ω)
LPH φ(ω) се конструира от точки. Характерните му точки: φ(0)=90°; φ(ωs)=45°; φ(∞)=0.
Интегриращата връзка.LAH (фиг. 9.29) е права линия, минаваща през точката ω = 1 на разстояние 20lgkот оста x и имаща наклон от -20 dB/dec. LPH се изразява като права линия, успоредна на абсцисната ос и отдалечена от нея на разстояние -π / 2 (-90 °).
Забавена връзка. Уравненията на логаритмичните амплитудни и фазови характеристики на тази връзка съответно имат форматаL(ω)= 20lgk; φ(ω) = - ωτ.
По този начин LAC на забавената връзка е подобен на LAC на безинерционната връзка, а LPH е крива с неограничено увеличение на ъгъла φ(ω), тъй като честотата ω се променя от 0 до ∞.
Тестови въпроси
1. Какви са статичните и динамичните режими на работа на обекта и какви са типичните смущаващи ефекти?
2. Какви реални физически обекти могат да бъдат представени чрез апериодична връзка? Каква е предавателната функция на апериодична връзка?
3. Какви са AFC и типичната крива на ускорение на апериодична връзка?
4. Какви обекти могат да бъдат представени като интегрираща (астатична) връзка? Каква е трансферната функция на такава връзка?
5. Какви са AFC и типичната крива на ускорение на интегратора?
6. Дайте примери за изпълнение на осцилаторни и апериодични връзки от 2-ри ред. Каква е предавателната функция на осцилаторна връзка?
7. Какво е AFC на осцилаторна връзка?
8. Какви са типичните криви на ускорение за осцилаторни и апериодичниВръзки от 2-ри ред?
9. Дайте примери за изпълнение на пропорционална връзка. Какви са AFC и типичната крива на ускорение на тази връзка?
10. Дайте пример за идеална разграничителна връзка. Каква е неговата трансферна функция?
11. Обяснете AFC и кривите на ускорение на идеалните и реалните диференциращи връзки?
12. Дайте пример за изпълнение и обяснете AFC и типичната крива на ускорение на изоставащата връзка.
13. Какви са логаритмичните честотни характеристики на динамичните връзки?
14. Обяснете LAH и LPH на инерционни и апериодични връзки?
15. Какви са LAH и LPH на осцилаторната връзка и какви фактори влияят върху промяната в тези характеристики?
16. Обяснете LAH и LPH на диференциращите и интегриращите връзки.
Глава 10
СВЪРЗВАНЕ НА ВРЪЗКИ В ACS
Типични връзки за връзки
В реалните промишлени ACS свързването на елементи заедно може да бъде доста сложно. Всяка сложна верига обаче може да бъде разделена на отделни блокове с една от трите типични връзки: последователна, паралелно съвпадаща или паралелно-противоположна.