Математически анализ на пазарите
Финансовите институции и корпорации, както и частните инвеститори и анализатори, често използват данни от финансови времеви редове (като цени на активи, обменни курсове, БВП, инфлация и други макроикономически показатели) в икономически прогнози, анализ на финансовите пазари или само по себе си извличане на данни.
Въпреки това, за да можете да приложите това към вашия анализ, правилното почистване на данните е от ключово значение. В тази статия ще ви покажем как да извлечете точно данните, които са подходящи за вашия анализ.
Сурови данни Точковите данни често са нестационарни или имат средни стойности, дисперсия и ковариация, които се променят с времето. Нестационарното поведение може да бъде свързано с тенденции, цикли, произволни движения или комбинация от трите.
Нестационарните данни обикновено са непредвидими и не могат да бъдат моделирани или прогнозирани. Следователно резултатите, получени с помощта на нестационарен времеви ред, могат да се окажат изкуствени - те могат да показват връзка между две променливи, когато такава по принцип не съществува. За да се получат последователни, надеждни резултати, нестационарните данни трябва да бъдат преобразувани в стационарни данни. За разлика от нестационарен процес, който има променлива вариация и средна стойност, която не остава близка или се връща към далечна средна стойност във времето, стационарният процес се променя около постоянна дългосрочна средна стойност и има постоянна разлика, независима от времето.
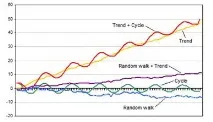
Видове нестационарни процеси Преди да стигнем до метода за трансформиране на нестационарни данни от финансови времеви редове, трябва да дефинирамеразлика между различните видове нестационарни процеси. Това ще ни даде по-добро разбиране на процесите и ще ни позволи да приложим правилната трансформация. Примери за нестационарни процеси са произволно движение със или без изместване (бавна постоянна промяна) и детерминистични тенденции (тенденции, които са постоянни, положителни или отрицателни, независимо от времето през жизнения цикъл на сериите от данни).
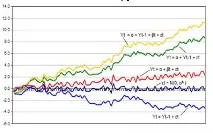
Чисто „случайно движение “ (Yt = Yf-l + εt) „Случайно движение“ прогнозира, че стойността в момента „t“ ще бъде равна на последната стойност на периода, който се изследва плюс стохастичен (несистематичен) компонент, който е бял шум, чиято стойност εt е независима и идентична на разпределение със средно „0“ и вариация „σ2“. Случайното движение може също да се нарече процес, включващ някакъв ред или процес със стохастична тенденция. Това не е процес на връщане на средната стойност, който може да се движи от средната стойност в положителна или отрицателна посока. Друга характеристика на произволното движение е, че разликата се развива с течение на времето и клони към безкрайност, докато времето се движи към безкрайност. Следователно произволното движение не може да бъде предвидено.
Изместване на произволно движение (Yt = a + βt+εt) Ако моделът на произволно движение прогнозира, че стойността в момента "t" ще бъде равна на стойността на предишния период плюс константа или изместване (α) и количеството бял шум (εt), тогава този процес е произволно изместване на движение. Освен това не се връща към дългосрочната средна стойност и има зависеща от времето вариация.
Детерминирантенденция) Случайното движение с изместване често се бърка с детерминирана тенденция. И двете включват изместване и компонент на бял шум, но стойността в момента "t" в случай на произволно движение регресира спрямо стойността на предходния период (Yt-1), докато в случай на детерминистична тенденция, тя регресира спрямо времевата тенденция (pt). Нестационарен процес с детерминистична тенденция има средна стойност, която нараства около фиксирана тенденция, която е постоянна и независима от времето.
Случайно движение с изместване и детерминистична тенденция Друг пример е нестационарен процес, който съчетава произволно движение с изместващ компонент (a) и детерминистична тенденция (pt). Той определя стойността в момент "t" в зависимост от стойността на предходния период, промяната, тенденцията и стохастичния компонент.
Тенденция и стационарна разлика Случайното движение със или без изместване може да се преобразува в постоянен процес чрез диференциране (като извадим Yt-1 от Yt, получаваме разликата Yt - Yt-1) и след това процесът става стационарна разлика. Недостатъкът на диференциацията е, че процесът губи една единица наблюдаеми данни всеки път, когато се вземе разлика.
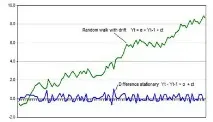
Нестационарен процес с детерминистичен тренд става стационарен след така наречения "detrend" или премахване на тренда. Нито една единица от наблюдаваните данни не се губи, когато премахването на тренда се използва за преобразуване на нестационарен процес в стационарен. В случай на произволно движение с изместване и детерминистична тенденция, чрез „отмяна на тренда“ е възможно да се премахне детерминистичната тенденция и изместване, но вариацията ще продължи да върви до безкрайност. В резултат на това трябвадиференцирането може да се приложи и за премахване на стохастичната тенденция.
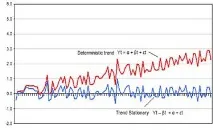
Заключение Използването на нестационарни времеви редове от данни във финансовите модели води до ненадеждни и изкуствени резултати и води до лошо разбиране и прогнозиране на протичащите процеси. Решението на този проблем е свързано с трансформирането на времевия ред от данни по такъв начин, че той да стане стационарен. Ако нестационарният процес е произволно движение със или без изместване, тогава той се трансформира в стационарен процес чрез диференциране. От друга страна, ако анализираните времеви редове от данни показват детерминистична тенденция, тогава изкуствените резултати могат да бъдат избегнати чрез премахване на тенденцията. Понякога нестационарна серия може да комбинира стохастична и детерминистична тенденция едновременно и трябва да се приложи диференциация и премахване на тренда, за да се избегне получаването на изкривени данни, тъй като диференцирането ще премахне тенденцията във вариацията, а „detrend“ ще премахне детерминистичната тенденция.