Метод на най-малките квадрати
Има експериментални точки. Изисква се да се изгради графика и да се извърши апроксимация чрез подскъпоценности. Въпрос: кой пакет може да го направи най-бързо? В Origin изобщо не намерих MNC
Ключовата дума е "fit". --- . Работя като антинаучен измамник.
График за какво? Вземете и свържете тези точки, тогава разликата ще бъде 0 Mb линейно приближение?
И аз знам. Само в Origin има три съвпадения: линейно, полиномиално и сигмоидално.
Подозирам, че и тримата --- младши Само с различни функции. --- . Работя като антинаучен измамник.
In-in. Това ми говори и това, което ми остана в главата от първата година.
Ето, мамка му, и обясни какво точно ти трябва.
Не, не си прав! Регресионното приспособяване е внедрено в началото! а не по метода mins
Необходимо е да се начертае апроксимираща крива, използвайки метода на най-малките квадрати за този боклук:
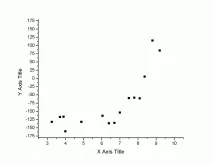
Какво е регресия? - MNK е.
Измислихте ли хипотеза? Каква кривина ще нарисувате? --- . Работя като антинаучен измамник.
Така че, ако сега 100% запомних най-малките квадрати, разбира се, ще има една крива. Какво означава какво?
но ако не се нуждаете от най-малки квадрати, а просто трябва да приближите експерименталните точки С някаква функция, тогава тя дава сравними резултати с най-малки квадрати! (от гледна точка на точност) но за това трябва да знаете предварително коя функция да апроксимирате!
да А защо тогава се казваше по друг начин?
значи просто трябва да начертаете красива крива през тези точки? Без да знаете нейната формула? Това не е приближение, а се нарича сплайн! Origin има само сплайн и бета сплайн - те са най-добрите!
Няма еднозначен отговор. Можете да направите приблизително права линияможе да е парабола, може да е експонента - методът винаги ще работи, просто картината може да се окаже тромава. Ако класът от функции, в които се произвежда LSM, не е известен предварително, той може да бъде измислен. Например, изглежда малко като парабола от 2-ри или 4-ти ред, така че можете да приложите полинома на най-малките квадрати от 2-ри или 4-ти ред
Yokarny bogeyman и няма книги за MNK под ръка. Е, от тези три, сигмоидното приближение е най-красивото
Те просто го взеха и го кръстиха.
значи просто трябва да начертаете красива крива през тези точки?
Да, и все още има разширение на тези три! Там можете да управлявате всяка функция! Нямате нужда от него и нямате нужда от книга за MNC! Направете сплайн! или b-сплайн! и ще бъдеш красива!
Вие сте мин. можете да поставите произволна крива. --- . Работя като антинаучен измамник.
Proyuzay всички и изберете кое е по-просто и по-добре. Повече или по-малко очевидно, ако размерът на функционален клас е > \infty , тогава получената крива ще бъде притисната към тези точки и всичко ще бъде тромаво.
Какво мислиш, че тогава е регресия? И между другото, линейна регресия ли имаш предвид или нещо друго?
Да, поне само линейно!
Каква функция трябва да бъде изградена?
Така че не можете да дадете определение за регресия. В общия случай можете да приложите различни видове регресия, но OLS е най-простият и разбираем дори за таралеж.
Да, просто не помня точно! и не искам да се хващаш за всякакви тънкости! Но регресията е числен метод, а методът на най-малките квадрати е аналитичен!
бройте всичко MS EXEL - така че прочетете помощта и не се притеснявайте!