Метод на режеща равнина
Този метод се използва за изграждане на линия на пресичане на повърхности, което ви позволява да получите (едновременно) във входните режещи равнини, графично прости линии (прави линии или кръгове). Това твърдение може да се илюстрира с примера на пресечната точка на цилиндъра ∆ и конуса Ф на фигура 8.25.
Фигура 8.25 - Метод на режеща равнина
Тук хоризонталните равнини на ниво Si действат като спомагателни секущи равнини. На повърхността на конуса (поради факта, че са перпендикулярни на оста на въртене), тези равнини разграничават кръгове, а на повърхността на цилиндъра - успоредни линии (генератори).
Характерните точки A, B на пресечната линия се определят в пресечната точка на челните очертания. Текущите точки на линията на пресичане ще бъдат определени като резултат от пресичането на съответните окръжности и линии в режещите равнини Si.
Сфери за рязане
Този метод се основава на факта, че две коаксиални повърхности на въртене се пресичат по окръжност, разположена в равнина, перпендикулярна на общата ос на въртене.
Една сфера ще бъде коаксиална с всяка повърхност на въртене, ако нейният център лежи върху оста на въртене на тази повърхност (Фигура 8.26). Това определя възможността за използване на сферата като спомагателна режеща повърхност.
Методът на режещата сфера се използва в следните случаи:
1. Помислете за повърхности на въртене, техните оси трябва да се пресичат в една точка - центърът на секущите сфери.В този случай е желателно равнината, образувана от пресичането на осите, да бъде успоредна на една от проекционните равнини.
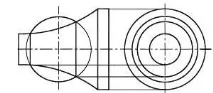
Фигура 8.26 - Пресичане на коаксиални повърхности
Линията на пресичане на два цилиндъра Ф и ∆ (RФ>R∆) може да се определи по метода на секущата сфера. Това се определя от факта, че всички по-гореусловия. Пресечната линия се разделя на два клона, долен и горен, чиято конструкция е подобна (Фигура 8.27). Фронталните проекции на характерните точки на пресечната линия 12 и 22 се определят в резултат на пресичането на фронталните характеристики Ф2 и ∆2, а хоризонталните се определят от принадлежността на тези точки към цилиндъра Ф.
Най-ниската точка на пресечната линия (3) се определя чрез въвеждане
сфера RФ, която ще пресича цилиндъра Ф по окръжността l (пред.
таличната проекция на този кръг ще съвпадне с фронталната проекция
сечение на оста на въртене на цилиндъра ∆).
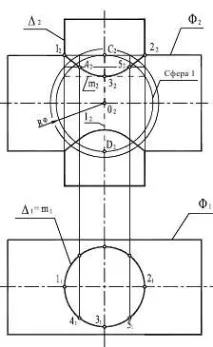
Фигура 8.27 - Методът на рязане на сфери
Същата сфера се пресича с цилиндъра ∆ по окръжността m. Точка 3 и Сфера 1 са резултат от пресичането на окръжности l и m. Междинните точки се определят подобно на пресечната точка на кръгове, получени при пресичането на произволни сфери RФ