Метод на спомагателните секущи сферични повърхнини, Дескриптивна геометрия
Методът на спомагателните секущи сферични повърхности ви позволява да определите линията на пресичане на две произволни повърхности на въртене. За това се използва свойството, присъщо на повърхностите на въртене - всеки две коаксиални повърхности на революция се пресичат по окръжност, минаваща през точките (A, B) на пресечната точка на техните меридиани (m1, m2).
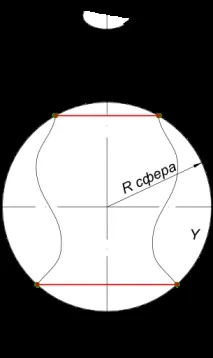
Равнините на кръговете на сечението са перпендикулярни на оста на повърхността на въртене. Следователно, ако осите на повърхностите на въртене са успоредни на равнината на проекцията, тогава окръжностите на сечението се проектират върху тази равнина в сегменти, перпендикулярни на проекцията на оста на въртене върху нея. Като спомагателна секуща повърхност на въртене се използва сферична повърхност, удобна за рисуване, чийто център трябва да принадлежи на оста на повърхността на въртене. Задачите за определяне на линията на пресичане на две произволни повърхности на въртене, имащи обща равнина на симетрия, се решават просто с помощта на спомагателни сферични повърхности. В този случай се разграничават два случая: - ако осите на повърхнините се пресичат; - ако осите на повърхнините не се пресичат.
Осите на две произволни повърхности на въртене се пресичат
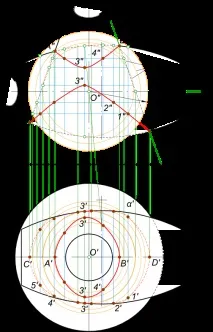
дефинирането на линията на пресичане на две повърхности на въртене се извършва с помощта на концентрични сфери. В този пример, това е конус и тороид (самосичащ се тор),се използва методът на спомагателните секущи сферични повърхности, които имат общ център. Използването на концентрични сфери е възможно при наличието на три графични условия: - повърхностите на въртене се пресичат (с изключение на отворен и затворен тор); - общата равнина на симетрия е равнината на нивото; - осите на повърхнините се пресичат в точка, която служи за общ центърспомагателни секущи сферични повърхнини. Тук не е рационално да се използва методът на спомагателни режещи равнини, тъй като нито една равнина на ниво не пресича повърхностите в кръгове. Алгоритъм за построяване на линията на пресичане: - намерете референтни точки A и B, C и D в пресечната точка на меридионални сечения m1 и m2 на повърхности α и β; - намиране на пресечната точка на осите на повърхнините α и β: О=(iα ∩ iβ); - начертаваме спомагателна сферична повърхнина Y с произволен радиус Р, която пресича повърхнините α и β съответно по окръжностите a=(α ∩ Y) и b=(β ∩ Y); - намерете точките на пресечната линия в пресечната точка на кръговете; - действайки по този начин, можете да намерите достатъчен брой точки, свързвайки които с гладка линия, получаваме желаната линия на пресичане на повърхностите.
Когато повърхностните оси не се пресичат
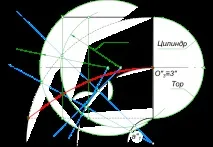
Изграждането на линията на пресичане на отворен тор и цилиндър се извършва с помощта на метода на ексцентричните сфери, тъй като: - отвореният тор има кръгови сечения във фронтално изпъкнали равнини, минаващи през неговата ос на въртене; - обща равнина на симетрия на повърхности; - кръстосани повърхностни оси
и се извършва по следния алгоритъм: - въвеждаме спомагателни сфери, задавайки произволни участъци от повърхността на тора чрез фронтално проектиращи се равнини, минаващи през неговата ос. Окръжността a1-a2 е дадена линия на пресичане на тора с желаната спомагателна сфера, чийто център трябва да лежи върху перпендикуляра на проекцията на тази окръжност; - провеждаме до правата a1-a2 през нейния среден перпендикуляр на и при пресичането му с оста на цилиндъра намираме центъра O1 на спомагателната сфера; - от центъра O1 чертаем окръжност с радиус Rsf1; - изграждаме линията на пресичане sf1 с цилиндър b1-b2; - при пресичането на a1-a2 и b1-b2 намираме съвпадащите точки 1(1);- действайки по този начин, можете да намерите достатъчен брой точки, свързвайки които с гладка линия, получаваме желаната линия на пресичане на повърхностите.