Метод Румянцев - 6 стр
тогава уравнение (3.4) няма корени,
(a) > 0, P n (a)>gt; 0,
И все пак най-голям интерес за нас представляват неалгебричните уравнения, т.е. уравнения от най-общ вид (3.3). В този случай графичните методи за локализиране на корена са много ефективни.
3. Графична локализация на корените
За да намерите груби приблизителни стойности на реалните корени на уравнение (3.3), можете да начертаете функцията y \u003d f ( x ) и да намерите абсцисите на точките на пресичане на графиката с оста x (фиг. 3.3). Понякога е по-удобно първо да представите уравнението във формата
Помислете за следния пример. Нека е необходимо да се намерят корените на уравнението
Тъй като x = 0 не е корен на това уравнение, ние го представяме във формата
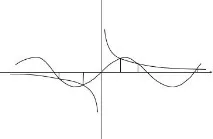
и начертайте графиките на функциите от лявата и дясната страна на това уравнение
г
Корените на уравнението са симетрични по отношение на x = 0, така че можем да разглеждаме само положителни корени (съответните отрицателни корени се различават от положителните само по знак). Стойностите на x 1, x 2 и още няколко корена могат да бъдат определени графично доста точно, но е невъзможно да се изобразят всички корени на x n на графика. В същото време в хода на класациите
очевидно е, че за големи n стойностите на x n ще бъдат близки до π n.
В този случай можем да приемем, че за всички n, започвайки поне от
четвърто, условията
x n [ π n − ε ; π n + ε],
където ε > 0 е някакво не твърде малко число (достатъчно за лявата страна на сегментите (3.6), за дауравнение (3.5) взе стойности с различни знаци). Съотношения (3.6) са желаните достатъчно малки области, всяка от които съдържа един и само един корен на уравнение (3.5). По този начин положителните корени на уравнение (3.5) са разделени и локализирани чрез отношения (3.6).
В анализирания пример използвахме знанията си за свойствата на функциите, включени в лявата страна на уравнение (3.5). Как да бъдем в тези случаи, когато тези функции са много и са сложни? В тези случаи можем да предложим следната схема на действие, която по същество е много близка до графичния метод за разделяне на корените.
В практическите приложения количествата, които ни интересуват (неизвестни, влизащи в уравнения), не могат да приемат произволно големи или произволно малки стойности. Зоната на промяна на неизвестното винаги е ограничена както отдолу, така и отгоре и тези ограничения по никакъв начин не са свързани с зоната на оп.
определяне на функциите, включени в уравнението (по това приложните задачи, разглеждани в този курс, се различават от „чисто математическите“). За уравнение с едно неизвестно тази област е числов интервал или набор от няколко интервала (ако има точки или набори от точки вътре в областта на промяна на неизвестното, при които функциите, включени в уравнението, не са дефинирани).
Нека разделим тази област на секции по точки x n , n = 1, …, N и изчислим стойностите f ( x n ) на лявата страна на уравнение (3.3) в точките на разделяне. Ако стъпката на разделяне е достатъчно малка *, тогава можем да предположим, че уравнението има точно толкова корени, колкото пъти се променя знакът на f ( x n ). Съгласно основната теорема, всички тези корени ще бъдат локализирани в тези секции на дяла, където функцията f ( x ) променя знака. След като корените се отделят и локализират, те започват да ги прецизират.
§ 2. Някоиитеративни методи за рафиниране на корени
Методите за прецизиране на корените на нелинейните уравнения се основават, като правило, на използването на итеративни изчислителни алгоритми, които се сближават до желания корен. Срещнахме такива алгоритми в първата глава (§3). Сега ще продължим запознаването си с тях чрез примера за решаване на нелинейни уравнения от общ вид (3.3).
Нека коренът на уравнение (3.3) е локализиран върху сегмента [ a , b ]. Изисква се да се определи стойността на този корен с дадена точност ε > 0, т.е. намери един
числото x *, за което условието е вярно