Модел Cournot
Един от първите модели на олигопола е дуополният модел (две фирми в индустрията), предложен от френския икономист Курно през 1838 г. Този модел се основава на три предпоставки: 1) има само две фирми в индустрията; 2) за всеки олигополист пазарният обем не е постоянна стойност, а пряко зависи от решенията на конкурентите; 3) и двете фирми максимизират печалбите.
На графиката (Фигура 4.30) продукцията на фирма № 1 е представена като функция на продукцията на фирма № 2, а продукцията на фирма № 2 е представена като функция на продукцията на № 1. Продукцията на една фирма, изобразена като крива, е представена като отговор на продукцията на друга фирма.
Да видим дали и двете фирми могат да установят взаимно приемливи производствени обеми. Да приемем, че фирма №2 ще произведе 75 единици, в който случай фирма №1 ще реши да произведе 12 единици (виж точка А). Но ако Фирма #1 наистина издава 12 единици, тогава, както е показано на графиката, Фирма #2, според нейната крива на реакция, трябва да издава не 75, а 42 единици (виж точка B). Но това ниво на продукция от конкурент ще принуди фирма 1 да произведе не 12 единици, както е възнамерявала, а 29 единици (виж точка C).
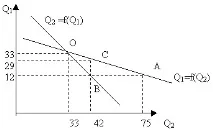
Ориз. 4.30. Модел Cournot
Лесно е да се види, че нивото на производство, зададено от компанията въз основа на съществуващия размер на производството на конкурента, всеки път се оказва такова, че принуждава последния да го преразгледа. Това предизвиква нова корекция в продукцията на първата фирма, която от своя страна отново променя плановете на втората, т.е. ситуацията е нестабилна, неравновесна.
Съществува обаче и точка на стабилно равновесие - това е точката на пресичане на реакционните криви на двете фирми (точка О на графиката). В нашия пример равновесиетообемът на производството е 33 бр. При това ниво на производство всяка фирма максимизира печалбата. Тази ситуация се нарича в икономическата теория на равновесие на Курно.
Равновесието на Курно се разбира като такава комбинация от обемите на продукцията на всяка от фирмите, при която нито една от тях няма стимули да промени решението си: печалбата на всяка фирма е максимална, при условие че конкурентът поддържа този обем на продукцията.
Математически теорията на игрите показва, че равновесието на Курно се постига при някои допускания за логиката на поведението на дуополистите, но не и при други. В същото време яснотата (предвидимостта) на действията на партньора-състезател и неговата готовност за съвместно поведение със съперника е от решаващо значение за постигане на равновесие.
Разбира се, моделът на Курно изглежда малко опростен, но обръща внимание на силната взаимозависимост на поведението при олигопол.
Теория на играта
Теорията на игрите е разработена от Джон фон Нойман и Оскар Моргенщерн през 1944 г.
Теорията на игрите разглежда пазарното поведение като игра, в която участват лицата, вземащи решения; има определени правила на играта; според резултатите от играта се присъждат награди или дузпи. Когато взема решение за игра, участникът не знае със сигурност каква стратегия ще избере опонентът му, той може само да прави прогнози.
Аналог на такава игрова ситуация е така наречената „дилема на затворника“. В таблицата е представена матрицата на наградите-глоби за двама затворници, обвинени по едно дело.
Да предположим, че затворниците не могат да се споразумеят и да изберат най-изгодната за всеки от тях стратегия на поведение - да не признават деянията си и да получат само по косвени доказателства 1 година лишаване от свобода. Какво може да е поведението (и неговите резултати)затворник, когато реакцията на втория участник в играта е неизвестна?
Има стратегии на поведение, известни като максимин и максимакс.
Максималната стратегия характеризира песимистичния възглед за живота, когато участник в играта А вярва, че противникът Б ще действа по най-лошия начин за А. В представената в таблицата матрица най-лошият вариант е лишаване от свобода за 10 години. При условие, че А не е в съзнание, но Б е в съзнание. За да избегне това и да си осигури най-малко лошия от всички лоши резултати, А решава да си признае: в този случай най-лошото би било да получи 5 години затвор; но този лош резултат ще бъде по-добър от 10 години затвор, ако А не си признае. Затворник Б ще разсъждава по подобен начин.В резултат на това, без да са съгласни, и двамата затворници ще стигнат до решението да си признаят.
Стратегията maximax се избира от оптимисти, които се надяват, че техният опонент ще им помогне да постигнат най-добър резултат. Така. оптимистичният затворник А очаква най-добрия резултат за себе си - да бъде освободен. Той се надява, че затворник Б няма да си признае, така че самият той признава вината си. Въпреки това, затворник B също е оптимист по природа и също иска да бъде свободен. Той от своя страна смята, че А не си признава, така че затворник Б се разкайва за постъпката си. В резултат и двамата затворници си признават и получават 5 години затвор.
И двата пъти в нашия пример играчите стигнаха до един и същ резултат и се озоваха в долния десен ъгъл на матрицата награда-наказание. Този резултат се нарича "решението на Наш" (на името на носителя на Нобелова награда) или "равновесие на Наш". Условието на това равновесие е: ако е дадена стратегията на първия играч, вторият играч може само да повтори хода на първия и обратно.
Стратегията на фирма Б
Стратегията на фирма А
Моделът на поведение на фирмата става много по-сложен, акоброя на играчите и броя на реалните стратегии на поведение. Следователно възможностите на теорията на игрите не са безкрайни. Със сигурност може да се каже, че теорията на игрите още веднъж потвърждава взаимозависимостта на поведението на олигополните фирми.
Модел на конкурентни пазари.
Това е сравнително нова концепция. Неговата основна предпоставка е, че влизането и излизането от една индустрия не струва нищо. Веднага трябва да се отбележи, че на практика тази ситуация не се среща често. Както откриването на нова фирма, така и нейната ликвидация често са свързани със значителни разходи. Ако приемем това предположение, тогава появата на нови фирми на пазара става много вероятна.
Следователно, дори много големи олигополни фирми са постоянно застрашени от появата на конкуренти и загубата на тяхната пазарна мощ. В резултат на това заплахата от конкуренцията действа не по-малко от самата конкуренция, намалявайки нивото на разходите, понижавайки нивото на цените, увеличавайки производството и намалявайки икономическата печалба.