Монотонни функции
Функционални класове на логическата алгебра
В гл. 4 беше въведена концепцията за затворено множество, клас, генериращо множество на клас и база. Нека разгледаме тези концепции във връзка с набора FAL.
Върху множеството от функции F въвеждаме операцията на суперпозиция на функции, която се състои в замяна на някои аргументи на една отfОFс функции отF. Резултатът е нова функция, генерирана от суперпозицията. В този случай ще приемем, че в общия случай всички аргументи на функциите са различни, в частния случай наборите от аргументи на функцията могат да се пресичат или съвпадат. Получената функция може да се използва отново в суперпозиция и т.н.
Пример. НекаF=x&yy, xx®yy>. Резултатът от суперпозицията може да бъде функция x®(yy×z)
Наборът от всички функции, които могат да бъдат генерирани от суперпозиция на функции от набораF, ще се наричаклас от функции, генериран отFи означен като 1F1. МножествотоFсе наричагенериращомножество от клас ½F½
Генериращ набор от даден клас се наричабаза, ако нито едно подходящо подмножество от този клас не генерира този клас.
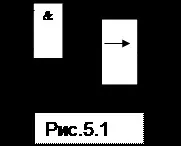
За примера, разгледан по-горе, веригата е показана на фиг. 5.1.
Нека разгледаме основните класове функции на алгебрата на логиката.
Ако a³ b и b³ a, множествата се считат занесравними.
ПримерПример. Множествата a= и b= са сравними и a³b. Множеството a и c= са несравними.
Дефиниция.Функцияfсе нарича монотонен, ако за всеки два набора от стойности на входните променливи a и b фактът, че a³b предполага, чеf(a)³f(b).
Свойства на монотонните функции.
Нулевият набор от стойности е сравним с всеки набор и е по-малък от който и да е от тях. Следователно, ако една монотонна функция е равна на единица в това множество, тогава тя е равна на единица във всяко множество, т.е. е равно на константа. По същия начин, ако една монотонна функция е равна на нула в набора от стойности за идентичност, тогава тя не може да бъде единица в нито един набор, тъй като наборът за идентичност е по-голям от всеки друг набор.
Нека функцията върху множество a, която е различна от единичната, е равна на 1 и нека стойността наi-тата компонента в нея е равна на 0. Това означава, че върху множеството, което се различава само по това, чеi-та променлива в него е равна на 1, функцията също ще приеме единична стойност. Това означава, че конюнкциите в DNF, съответстващи на тези множества, могат да бъдат слепени от променливата xxi. По същия начин, за набор със стойност на променлива 0 (т.е. с възможна стойност във връзката на променлива с инверсия), има набор със стойност на променлива 1, което ще доведе до залепване на тази променлива. Следователно,няма променливи в обратна форма в минималната DNF на монотонна функция.
2. От това свойство можем да заключим, че суперпозицията на монотонни функции отново ще бъде монотонна функция, т.е. набор от монотонни функции образува клас от монотонни функции, означен като M. Основата на класа M се формира както от константи, така и от двойка функции - конюнкция и дизюнкция, т.е. задайте x×yy, xxÚyy, 0,1>.
Проблем.Докажете, че константите трябва да присъстват в основата.
5.6.2. Самодвойни функции
Обозначете двойствената функция катоf*.
ПримерПример. За функция (x×y)двойната функция ще бъде (`xÚ`y) =xÚy.
Може да се покаже, че двойствената функция наf* ще бъде функциятаf, така че заxÚyдвойствената функция ще бъдеx×y.
Двойната наxще бъде функция, равна на x, двойната на 0 ще бъде 1.
Определение. Една функция се наричасамодуална, ако е равна на своята двойна.
Променливата x е пример за самодуална функция, както и обратната на променливата.
Свойства на самодуални функции.
1. Самодуалната функция се определя напълно от външния й вид в горната половина на таблицата на истината. Наистина, ако, например, стойността на функция в множеството 1, a2, …, an> е 0, тогава стойността на функцията на обратния набор трябва да бъде равна на 1.
2. От първото свойство следва, че броят на различните функции на n променливи е 2 m , където m=2 n -1 .
| Таблица 5.11 | |||||
| х | при | f1 | f2 | f3 | f4 |
3.Нека конструираме всички функции от две променливи. Ще има 4 от тях в съответствие с възможните стойности в горната половина на таблицата: 00,01,10,11. Тези функции са показани в таблица 5.11. Както се вижда от таблицата, първите две функции съвпадат с променливи, последните две - с инверсии на променливи. Това предполага следното свойство:няма самодуални функции, които по същество зависят точно от две променливи.
4. SDNF на самодуална функция ще има точно 2 n -1 конюнкции.
5. Суперпозицията на самодуални функции ще бъде самодуална функция. Наборът от самодуални функции образува клас, който обикновено се означава катоD. Основата на класа е функция от три променливи x×`yyÚxx×`z Ú`yy×`z>.