Московски десетокласник изпревари Ердош в построяването на остроъгълни триъгълници
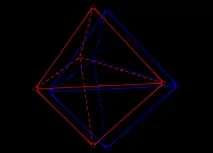
Идеята на доказателството е да се удвоят и леко да се изместят точките на „острия набор“ с всяко добавяне на две нови измерения.
Проблемът на Данцер и Грюнбаум е формулиран много просто - кой е най-големият брой точки в пространството, които могат да бъдат поставени така, че всеки три от тях да образуват остроъгълен триъгълник. Очевидно на равнината това число е равно на три (всеки опит да поставите четвъртата точка ще доведе до тъп ъгъл). За триизмерното пространство това число е равно на пет. За пространства с по-високо измерение такова число не е точно известно.
Според един от участниците в дискусията във Facebook, Александър Полянски, първоначално Дмитрий Захаров, независимо от Харанга, е получил същото подобрение (до около c × 1,2 N). Въпреки това Андрей Райгородски, на когото Дмитрий каза за резултата, откри статията на Харанга и „разстрои Дима“. Въпреки това математикът не се отказа и намери коренно различен подход към проблема. Конструкцията, използвана от ученика, дава възможност за създаване на "остри комплекти" от 2 N/2 точки. Както отбелязват участниците в дискусията, решението на Захаров е съвсем просто – отнема само половин страница.
Доказателството се основава на метода на математическата индукция. Да предположим, че за измерение N можем да конструираме "остър набор" от максималния брой точки (за N=2 и 3 можем да направим това). Нека покажем как да конструираме "остър набор" от два пъти повече точки за пространство с размерност N + 2. За да направим това, внимателно разделяме всяка точка от първоначалния набор, така че разстоянието между две нови точки да не надвишава определена стойност. В този случай ще направим всички бифуркации малко по-различни една от друга в проекцията върху равнината на две нови измерения. Тогава, ако стойността е избрана правилно (а това е винагиможе да се направи), новият комплект също ще бъде „остър“. Това удвояване може да продължи до безкрайност.
Важно е да се отбележи, че конструираният пример не дава отговор на въпроса какъв е максималният брой точки в "остър набор" за дадено измерение. Освен това това число е известно само в равнинното и триизмерното пространство, а за четири-, пет- и шестизмерните пространства няма точен отговор. Известно е, че "острото множество" е крайно за всяко измерение - броят на точките в него трябва да бъде по-малък от броя на върховете в куба на съответното измерение (2 N ).
По-рано съобщихме за британски ученик, който откри нова екзопланета на петнадесетгодишна възраст въз основа на анализа на данни от астрономическото проучване WASP.