Нотация

r– радиус на успоредната окръжност, mm;

h– дебелина на корпуса, mm;

m– моментно натоварване, равномерно разпределено по обиколката, N*mm/mm;

P– радиално натоварване, равномерно разпределено по обиколката, N/mm;

q– натоварване, разпределено върху площта, MPa;

Ns – нормална меридионална сила, N/mm;

Nt – нормална пръстеновидна сила, N/mm;

Ms – меридионален огъващ момент, N*mm/mm;

Mt – огъващ момент на пръстена, N*mm/mm;

Q– напречна сила, N/mm;

s – нормално меридионално напрежение, MPa;

t – пръстеновидно меридионално напрежение, MPa;

 – радиално преместване, mm;

 – ъгъл на завъртане на нормалата към средната повърхност на черупката, rad;

s * ,t * – нормални меридионални и обръчови напрежения, изчислени по безмоментната теория, MPa;

 * ,* – радиални и ъглови премествания, изчислени по безмоментната теория;

Pz – аксиално резултатно външно натоварване върху корпуса, N;

E– модул на еластичност на материала на обвивката, MPa;

 – Коефициентът на Поасон на материала на обвивката.

1. Основни понятия и определения

Подчерупкасе разбира тяло, чиито един размер – дебелина – е много по-малък от другите два. Геометричното място на точките, еднакво отдалечени от двете повърхности на черупката, се наричамедианна повърхност.Аксиално симетричниили простосиметричничерупки (черупки на въртене.) са тези, чиято средна повърхност е повърхност на въртене(Фиг. 1).

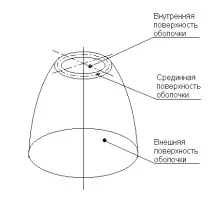
Фиг. 1. Тънкостенна обвивка на въртене

По-нататък ще разгледаме осесиметрични черупки с постоянна дебелина, малки в сравнение с размерите на черупката. Приемаме също, че натоварването, действащо върху черупката, също е осесиметрично. За такива черупки изчислителната задача е значително опростена поради факта, че вътрешните сили и премествания, възникващи в черупката, се променят само по протежение на генератора, оставайки непроменени в периферната посока.

2. Основни сведения за геометрията на повърхностите на въртене

Равнинна крива, чието въртене около определена ос образува повърхност, се наричапораждаща, нейните пресечни точки с оста на въртене се наричат ​​полюси. Крива, образувана върху повърхност от част от нейната равнина, минаваща през оста, се наричамеридиан. Очевидно меридианите съвпадат с генераторите. Равнините, перпендикулярни на оста на въртене, пресичат повърхността в кръгове, наречени успоредни кръгове.

Начертайте нормалатаn–nкъм повърхността в някаква точкаP(фиг. 2). Куп равнини, минаващи през нормалата, пресичат повърхността по линии, нареченинормални сечения. Радиусите на кривина на тези сечения в точкатаРкато цяло ще бъдат различни.

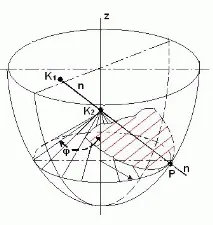
Фиг.2. Повърхност на въртене

Очевидно повърхностният меридиан също е нормален участък. Меридианът и нормалното сечение на повърхността с равнина, перпендикулярна на меридиана (перпендикулярна на допирателната към меридиана в точкаР) се различават по това, че от всички нормални сечения в тази точка имат най-големия и най-малкия радиус на кривина.

Радиусът на кривината на меридиана се наричапървият основен радиус на кривинаR1 на повърхността в дадена точка (отсечката от нормалатаК1Рна фиг.2), радиусът на кривина на нормално сечение от равнина, перпендикулярна на меридиана, евторият основен радиус на кривинаR2 повърхности в тази точка (отсечката от нормалатаК2Рмежду точкатаРи оста на въртене на повърхността на фиг.2). Центровете на кривинаК1 иК2 лежат върху нормалата към повърхността в тази точка, а вторият център на кривинаК2 на повърхността на въртене лежи върху оста на въртене, както е доказано в диференциалната геометрия.

Нормалите, начертани към повърхността в точките на успоредната окръжност, се пресичат в една точка, лежаща на оста на въртене, и образуват конична повърхност, нормална към разглежданата повърхност.

Радиусът на успоредната окръжностrе свързан с втория главен радиус на кривина чрез очевидната зависимост:

, (1)

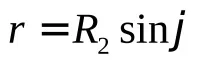
където

е ъгълът между нормалата на повърхността и оста на въртене.

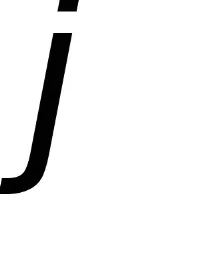
Сега можем да дадем по-точна дефиниция на понятието тънка черупка. Черупките се считат за тънкостенни, ако съотношението

е изпълнено, къдетоhе дебелината на черупката,Rmin = min(R1,R2).

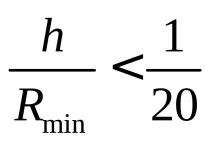
В теорията на черупките е доказано, че относителната грешка при изчисление не надвишава

. Следователно, приемайки горното съотношение, ние предоставяме обичайната точност на изчислението за технически проблеми.

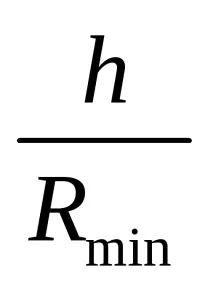
В зависимост от формата на средната повърхност черупките се делят на цилиндрични, конични, сферични и др. и т.н.

---