Оптимум, оптималност - Речник на Лопатников
Оптимум, оптималност [оптимум, оптималност] - от гледна точка на математиката, оптимумът на функция е нейната екстремна стойност (виж Екстремум на функцията), която е по-голяма от другите стойности на същата функция - тогава това е глобален или, по-добре, абсолютен максимум, или по-малко от други стойности - тогава това е глобален (абсолютен) минимум. Ако тълкуваме най-голямата или най-малката стойност на някои икономически характеристики като най-добри (в един или друг смисъл), тогава ще стигнем до основните понятия на икономическите и математическите методи - понятията за оптимум и оптималност.
Терминът „оптимум” се използва поне в три смисъла: 1) най-добрият възможен вариант на възможните състояния на системата – търси се чрез „решаване на задачи на О.”; 2) най-добрата посока на промени (поведение) на системата („отидете на O.”); 3) целта на развитието, когато говорят за "постигане на О.". Терминът "оптималност", "оптималност" означава характеристика на качеството на взетите решения (оптимално решение на проблема, оптимален план, оптимално управление), характеристика на състоянието на системата или нейното поведение (оптимална траектория, оптимално разпределение на ресурсите, оптимално функциониране на системата) и др.
Това не са абсолютни понятия: не може да се говори за оптималност изобщо, без условия и без точно определени критерии за оптималност. Решение, което е най-добро при определени условия и от гледна точка на един критерий, може да се окаже далеч от най-доброто при други условия и според друг критерий. Освен това трябва да се отбележи, че в реалната икономика, тъй като тя е вероятностна по природа, оптималното решение не е непременно най-доброто. Трябва също така да вземем предвид коефициента на стабилност на решението. Може да се окаже, че оптималният план за изчисление е нестабилен: всеки, дорилеки отклонения от него могат да доведат до рязко негативни последици. И би било препоръчително да се приеме не оптимален, но стабилен план, отклоненията от който ще се окажат не толкова опасни. (Лесно се вижда, че тук се извършва известна подмяна на критериите: вместо критерия за максимума на разглеждания индикатор се въвежда критерият за надеждността на плана).
- · В обща задача на математическото програмиране, вектор от инструментални променливи е точка от глобалното O. (решение на проблема), ако принадлежи на допустимо множество и целевата функция приема в това множество стойност, която не е по-малка (за максимална задача) или не повече (за минимална задача), отколкото във всяка друга допустима точка (вижте Екстремум на функция). Според точката на местния О . е вектор от инструментални променливи, принадлежащи към допустимото множество, на което стойността на функцията е по-голяма (по-малка) или равна на стойностите на функцията в някакъв малък квартал на този вектор. Очевидно е, че глобалното О. също е локално, докато обратното твърдение би било невярно. За функция на една променлива това може да бъде показано на фиг. 0.9, където F (x) = y е целевата функция, x е инструменталната променлива.
Тест за оптималност, следващ от казаното: ако малко движение от изпитваната точка намалява (за задачата за максимизиране) целевата функция (функционал), тогава това е O. Такова правило обаче се прилага само за изпъкнала област от възможни решения. Ако не е изпъкнала, тогава дадената точка може да бъде само локална точка (вижте Градиентни методи).
Различават се два вида оптимални точки: вътрешни и гранични точки (на фиг. 0.9 точката x3 е локална гранична точка, точките x1, x2 са вътрешни локални точки, а x* е вътрешна глобална точка). В първия случай е възможнонамиране на O. чрез диференциране на функцията и приравняване на производната на нула (или частни производни за функция на много променливи). Във втория случай този метод е неприложим (неприложим е и ако функцията не е гладка (вижте Плавна функция).
Ако оптималната точка е уникална, тогава имаме силно O. , в противен случай имаме слабо O. Съответните условия се прилагат както за глобални (абсолютни), така и за локални O.
Вижте Глобален критерий, Национален икономически критерий за оптималност, Оптимално функциониране на икономическата система, Оптималност по Парето, Принцип на оптималност, Социално-икономически критерий за оптималност.
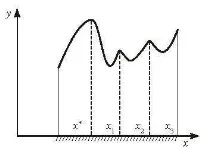
Фиг. O.9 Глобални и локални оптимуми
Знаеш ли това:
Смята се, че САЩ в процеса на външнотърговския обмен „изнасят“ капитали и „внасят“ труд. Американският икономист и нобелов лауреат В. Леонтиев установи, че това не е така.