Основи на изчислението на конусни трошачки
Условията за раздробяване на парче материал в конусни трошачки са подобни на условията за раздробяване в челюстни трошачки, така че методите за изчисляване на технологичните параметри на тези машини са до голяма степен подобни на разглежданите. Изчислителната схема на конусната трошачка е показана на фиг. 35.
Ориз. 34. Челюстна конусна трошачка
Ъгълът на захващане в конусните трошачки, т.е. ъгълът между трошачните повърхности на подвижния и неподвижния конус, както и в челюстните трошачки, не трябва да надвишава двойния ъгъл на триене, т.е. За конусни трошачки с грубо раздробяване ъгълът на захващане е 21–23 °, за трошачки със средно и фино раздробяване, 12–18 °, в зависимост от вида на облицовката.
Честотата на въртене на ексцентричната втулкаnв rpm за трошачките KKD се определя по същия начин както за челюстните трошачки, т.е. от условието за осигуряване на пътяhна свободно падащо парче натрошен материал за времетоt, през което ексцентричната втулка прави половин оборот:
От диаграмата (фиг. 35) следва:
Фиг.
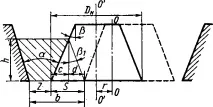
където r е ексцентрицитетът, разстоянието от оста на трошачката ОО до оста на конуса О'О';
Замествайки тази стойностhвъв формула (21), получаваме:
Тъй като всъщност материалът се забавя срещу стените на конусите и скоростта на движението му намалява, се препоръчва скоростта на въртене, получена по формула (22), да се намали с около 10%.
След като приехме това изменение, най-накрая получаваме скоростта на въртене на ексцентричния ръкав за трошачки KKD:
За да се определи скоростта на въртене на ексцентричната втулка на трошачките KSD и KMD, се приема, че:
парче натрошен материал в камерата за раздробяване се плъзга под действието на гравитацията по наклонената повърхност на раздробяванетоконус;
по време на преминаването на паралелната зона, парче натрошен материал трябва да бъде компресирано поне веднъж от смачкващите повърхности на конусите.
Ако ъгълът между образуващата на трошачния конус и основата еy(фиг. 36, а), тогава по време на работа на трошачката ъгълът на наклона на повърхността на трошачния конус спрямо хоризонта се променя отy- p доy+ p. При извеждането на формулата може да се вземе средният ъгъл на наклона, т.е.y. Силите, действащи върху парче натрошен материал
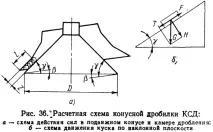
материалите в камерата за раздробяване са показани на фиг. 36,b. Силата на триенеF=fH=fGcosγ(тукfе коефициентът на триене на парчета материал по повърхността на конусите) е насочена в посока, обратна на плъзгането.
Силата, която насърчава движението на парче материал по наклонена равнина:
къдетоGе гравитационната сила на парче материал;Tе компонентът на гравитацията.
Тази сила не се променя, следователно под действието на нейното парче ще се движи равномерно ускорено. Акоαе ускорението на парчето, тогава:
Къде е скоростта на парчето:
Когатоt=0, скоростта на парчетоυсъщо е равна на нула, което означава, че константата на интегриранеС= 0. Тъй като
тогава начинът
КонстантатаC1 също е равна на 0, тъй като заt=0,S= 0. Време на един оборот на ексцентричната втулкаt= 1/n. През това време, според началните условия, парче материал трябва да измине път, равен или по-малък от дължината на паралелната зонаl≥S. Тогава
Дължината на паралелната зона за трошачки със средно раздробяване се приема като правило равна на 1/12D, къдетоDе диаметърътподвижен конус (фиг. 36,a).След това накрая скоростта на ексцентричната втулка за секунда:
За конусните трошачки с фино раздробяване се приема, че скоростта на въртене на ексцентричната втулка е същата като за трошачките със средно раздробяване, въпреки че дължината на паралелната зона в трошачките KMD е много по-голяма, отколкото в KSD. Парче материал, движещо се към изходната междина, се компресира няколко пъти чрез смачкване на конуси.
Ефективността на конусните трошачкиза едро трошене (фиг. 35) се определя при условие, че при едно завъртане на вала от трошачката изпада пръстен от материал с напречно сечение (m 2 ).
къдетоhе височината на пръстена, m;
Средният диаметър на падащия пръстен се приема приблизително равен на диаметъра на подвижния конус в долната DH, след което пръстенът се събаря (m 3 )
къдетоzе размерът на изходната междина (размерът на изходната междина за конусни трошачки е разстоянието между конусите за раздробяване при най-близкия им подход), m;r— ексцентрицитет на вала на нивото на изходния процеп, m;βиβ1са ъглите на образуващите на конуси за раздробяване спрямо вертикалата, град.
Капацитет на трошачката (m 3 /s)
къдетоVе обемът на материалния пръстен, който изпада при един оборот на втулката, m 3 ;μ—фактор на разхлабване на материала;n— скорост на втулката, об/мин.
Поставяйки стойносттаVот формула (23) в израз (24), получаваме производителността на едрите конусни трошачки (m 3 / s)
При изчисляване на производителността на конусните трошачки със средно раздробяване се приема, че при един оборот на ексцентричния ръкав парче материал преминава през дължината на паралелната зона, след което при един оборот част от материала с обем (m 3) се разтоварва от трошачката
къдетоzе ширината на паралелазони (ширина на изходния процеп), m;l- дължина на паралелната зона, m;Dcе диаметърът на кръга, описан от центъра на масата на материала, съдържащ се в паралелната зона.
къдетоμе коефициентът на разхлабване, равен на 0,45.
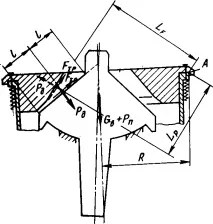
Резултантната сила на смачкванеза средни и фини трошачки се определя въз основа на силите, генерирани от предварително натоварени амортизиращи пружини. В същото време се приема, че силата на това затягане при нормална работа (фиг. 37. Схема за определяне на усилията
раздробяване в конусна трошачка
трошачката поддържа горната част на машината (опорния пръстен) в постоянен контакт с тялото на трошачката, т.е. силата на затягане се избира с определен запас в сравнение с действителните сили на смачкване.
Изчислителната схема за определяне на резултантната сила на смачкване Yad е показана на фиг. 37.
Подобно на челюстните трошачки, ние приемаме, че резултатът се прилага в точка, разположена в средата на зоната на трошене. Съгласно условието горната част на трошачката е в равновесие под действието на всички външни сили.
Уравнението на моментите на всички сили около точкаА
Откъдето максималната стойност на резултантните сили на смачкване (N)
къдетоGве силата на гравитацията на горната част на трошачката, N;РП—сила на предварително натягане на една пружина, N;n—брой пружини;R— разстояние от оста на трошачката до точкаA,m;LРиLF—рамена на силите спрямо точкатаА,m;f— коефициент на триене на подвижнотоконус върху натрошен материал.
Според изследване, проведено от проф. С. А. Панкратов и неговите ученици, резултатът от силите на смачкване (виж фиг. 39) е в равнината, минаваща през оста на подвижния конус, и тази равнина прави с равнината, минаваща през оста на подвижния конус и оста на трошачката, ъгъл а (фиг. 38), наречен водещ ъгъл.
Силата на смачкванеРdсе възприема от сферичния опорен лагер и ексцентричната втулка и предизвиква съответните реакцииRSFиRE.Когато конусът е в равновесие, линиите на действие на тези сили трябва да се пресичат на една точка. Познавайки резултанта на силите на смачкванеPdи точката на нейното приложение, както и вземайки позицията на реакцията на ексцентричната втулка в средата на височината на ексцентрика, ние определяме графично реакциите на сферичния опорен лагерRSFи ексцентрикаRЭ.
СилитеRd,RSFиREса изходни за изчисляване на якостта на елементите на трошачката. По време на работа на трошачката тези сили не остават постоянни, а се променят от минимални към максимални стойности.
За да определите средното усилие (N)при смачкване в трошачката KSD, можете да използвате емпиричната формула на проф. В. А. Олевски:
къдетоFе площта на страничната повърхност на конуса за раздробяване, m3.
Инерционни сили в конусните трошачки и тяхното балансиране.Конусната трошачка има две неуравновесени въртящи се маси: подвижен конус и ексцентрична втулка. По време на работа тези маси създават големи инерционни сили, които трябва да бъдат балансирани, за да се намали натоварването върху машинните части и основата.
При малки ъгли на въртене на конусаγ(в радиани) центробежна сила на инерцията на конуса: