Основи на класическата теория за електропроводимостта на металите на Друде-Лоренц
Многобройни експерименти показват, че носителите на ток в металите са свободни електрони, които могат да се движат почти свободно през метала. Съществуването на свободни електрони може да се обясни с факта, че по време на образуването на кристална решетка валентните електрони, които са най-слабо свързани с ядрото, се отделят от атомите, които стават „колективна собственост“ на целия кристал. Броят на електроните в единица обем е равен на броя на атомите в него, умножен по броя на валентните електрони, отделени от всеки атом.
Въз основа на концепцията за свободните електрони, Друде развива класическата теория за електрическата проводимост на металите, която след това е подобрена от Лоренц. На теория се приема, че електроните на проводимостта в металите се държат като молекули на идеален газ. В интервалите между сблъсъците те се движат напълно свободно, преминавайки средно по някакъв пътl, наречен среден свободен път. Вярно е, че за разлика от газовите молекули, чийто обхват е ограничен от сблъсъци на молекули една с друга, електроните се сблъскват главно с йони на кристалната решетка, а не помежду си. Тези сблъсъци водят до установяване на топлинно равновесие между електронния газ и кристалната решетка.
Общият заряд на електроните на проводимостта е равен по големина на общия заряд на положителните йони на кристалната решетка, което определя електрическата неутралност на кристала.
Поради произволността на топлинното движение на електроните, всички възможни посоки на техните скорости се срещат еднакво често, така че средната стойност на вектора на топлинната скорост на електроните е нула. Следователно при липса на външно електрическо полеобщият заряд, пренасян от електрони във всяка конкретна посока, е нула. Това означава, че при това условие в метала няма ток.
Ако върху метала се приложи външно електрическо поле с определена посока, тогава ускорените от полето електрони придобиват компоненти на скоростта, насочени към действието на силите на полето. Тези компоненти се наслагват върху скоростта на тяхното топлинно движение. В резултат на това всички електрони под действието на полето се изместват в посока, обратна на посоката на неговия интензитет, започва прехвърлянето на електрически заряд по протежение на проводника, т.е. възниква електрически ток.
Помислете за сегмент от проводника, чието напречно сечение е равно наS(фиг.
За период от времеdtпрез зонатаSще преминат всички онези заряди, които са на разстояние от зонатаS, т.е. всички заряди, съдържащи се в цилиндър с обем . Ако броят на свободните заряди (електрони на проводимост) на единица обем се означи сn, тогава общият зарядdq,, който ще премине през напречното сечение на проводника за това време, е равен на:
. (1)

Ориз. 1. Дрейф на електрони в електрическо поле
Силата на тока, протичащ в проводника, е
, (2)
и плътност на тока:
. (3)
Нека намерим средната скорост на дрейфа на електроните в електрическо поле от следното разсъждение.
Заряд, поставен в постоянно електрическо поле със сила, изпитва сила и в резултат на това придобива ускорение. Скоростта на електроните под действието на постоянна сила нараства линейно с времето. В края на свободния път обаче електронът се сблъсква с решетъчния йон, отдава енергията, придобита от него в полето, и скоростта му става равна на скоросттахаотично топлинно движение. Дори при много висока плътност на тока средната скорост на нареденото насочено движение на електроните под действието на електрическо поле е многократно (от порядъка на 10 8 ) по-малка от средната скорост на топлинно движение при обикновени температури.
10 -10 m = 1 Ǻ). До края на свободния път максималната скорост на насоченото движение на електрона е:
. (4)
Тогава средната стойност на насочената скорост на електроните по време на движение е половината от максималната; стойности:
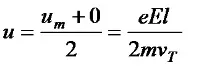
Замествайки (5) в (3), получаваме:
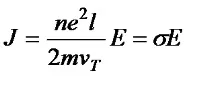
тези. Законът на Ом в диференциална форма.
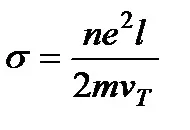
се нарича електрическа проводимост на метала. Специфичната електропроводимост на металите може да бъде представена в следната форма:
, (8)
където m е мобилността на токоносителите. Размерът му е m 2 / (V∙s). От (6) и (8) следва:
. (9)
Реципрочната стойност на s се нарича съпротивление r:
. (10)
Ако електроните не се сблъскват с йони, средният свободен път, а оттам и проводимостта, биха били безкрайно големи. Електрическото съпротивление се дължи на сблъсъци на свободни електрони с йони на кристалната решетка.
В полупроводниците електрическият ток се причинява от два вида носители на заряд: отрицателни - електрони и положителни - дупки. Следователно електрическата проводимост на полупроводниците може да се изрази чрез модифициране на формула (8):
, (единадесет)
къдетоeе модулът на заряд на електрон или дупка,nиpса концентрацията на електрони и дупки, съответно, иm-, m+са подвижността на електрони и дупки, съответно.