Основни операции върху множества

Ако A, B са множества, тогава има множество AB - обединение на множестваA и B, което се състои от всички елементи, които са елементи на множество A или множество B: AxB.

2.АкоA=R1nелемента. Следователно Булева често се наричастепен на наборAи се обозначава с2A.

Ако A, B са множества, тогава има тяхното директно (декартово) произведениеAB, състоящо се от всички подредени двойки(a;b), където aA,bB:

3.Ако множествотоAсе състои отmелемента, а множествотоB –отnелемента, тогава може да се докаже, че множествотоABсе състои отmnелемента. Поради тази причина в наименованието на комплектаАВсе използва терминът „продукт”. АкоA =B, тогава множествотоAAсе състои отm2елементи и се наричадекартов квадрат на множествотоAи се означава сA2.

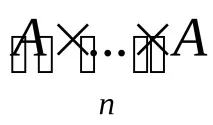
След декартовото произведение на две можете също да въведетедекартово произведениеA1…An=( … ((A1A2)A3)…)AnnнабориA1, … ,An. Множеството

се наричадекартова степен на множествотоAи се означава сAn.

Декартовият продуктAB =b)aAbB>от две множестваAиBпонякога условно се изобразява на равнина, третирайки компонентите на ред изддвойки(a;b)като координати:a–е координатата по остаx, върху която е маркирано множествотоA, аb–е координатата по остаy, върху което е маркирано множествотоB. Така елементите(a;b)АBса условно представени от точки на равнината с „координати”aиb.

Особено удобно е графичното представяне на декартовото произведениеABв случая, когатоAиB –са числови множества, т.е.AR,BR. Тогава изображението не придобива условен характер, а има много конкретно геометрично значение: множествотоABе множество от точкиM(a;b)от декартовата равнина, чиято първа координатаaпринадлежи на множествотоA, а вторатаb–принадлежи на множествотоB.

---