Основните свойства на функцията са четност, нечетност, периодичност, ограниченост
Функцията е едно от най-важните математически понятия. Функция - зависимостта на променливатаy от променливатаx, ако всяка стойностx съответства на една стойностy. Променливатаx се нарича независима променлива или аргумент. Променливатаy се нарича зависима променлива. Всички стойности на независимата променлива (променливаx ) формират обхвата на функцията. Всички стойности, които зависимата променлива (променливаy ) приема, формират диапазона на функцията.
Графиката на функция е набор от всички точки на координатната равнина, чиито абциси са равни на стойностите на аргумента, а ординатите са равни на съответните стойности на функцията, т.е. стойностите на променливатаx са нанесени по абсцисната ос, а стойностите на променливатаy са нанесени по ординатната ос . За да начертаете функция, трябва да знаете свойствата на функцията. Основните свойства на функцията ще бъдат разгледани по-долу!
Основни свойства на функциите.
1) Домейнът на функцията и обхватът на функцията.
Обхватът на функция е наборът от всички валидни стойности на аргументаx (променливаx ), за които е дефинирана функциятаy = f(x). Диапазонът на функция е множеството от всички реални стойностиy, които функцията приема.
В елементарната математика функциите се изучават само върху множеството от реални числа.
2) Функционални нули.
Стойностих, при коитоy=0, се наричат нули на функцията. Това са абсцисите на точките на пресичане на графиката на функцията с оста x.
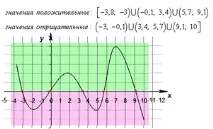
3) Интервали на постоянство на функцията.
Интервали на постоянство на функцията -такива интервали от стойностиx, на които стойностите на функциятаy са или само положителни, или само отрицателни, се наричат разстояния на постоянството на функцията.
4) Монотонност на функцията.
Нарастваща функция (в определен интервал) е функция, при която по-голяма стойност на аргумента от този интервал съответства на по-голяма стойност на функцията.
Намаляваща функция (в някакъв интервал) - функция, при която на по-голяма стойност на аргумента от този интервал съответства по-малка стойност на функцията.
5) Четна (нечетна) функция.
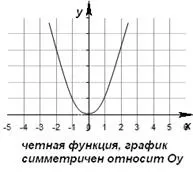
Четна функция е функция, чиято област на дефиниране е симетрична спрямо началото на координатите и за всеких от областта на дефиниция е вярно равенствотоf(-x) = f(x). Графиката на четната функция е симетрична спрямо оста y.
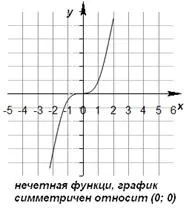
Нечетна функция е функция, чиято област на дефиниране е симетрична по отношение на началото на координатите и за всякоx от областта на дефиниция равенствотоf(-x) = - f(x ) е вярно. Графиката на нечетна функция е симетрична спрямо началото.
Една четна функция има следните свойства: 1) Областта на дефиниция е симетрична по отношение на точката (0; 0), т.е. ако точкатаa принадлежи на областта на дефиницията, тогава точката-a също принадлежи на областта на дефиницията. 2) За всяка стойностx, принадлежаща към областта на дефиницията, равенствотоf(-x)=f(x) 3) Графиката на четна функция е симетрична спрямо оста Oy.
Нечетната функция има следните свойства: 1) Областта на дефиниране е симетрична по отношение на точката (0; 0). 2) за всяка стойностx, принадлежаща към домейна на дефиницията, равенствотоf(-x)=-f(x) 3) Графика на странна функцияе симетричен спрямо началото (0; 0).
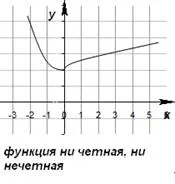
Не всяка функция е четна или нечетна. Функциитеот общ видне са нито четни, нито нечетни.
6) Ограничени и неограничени функции.
Една функция се нарича ограничена, ако съществува положително число M, такова че f(x) ≤ M за всички стойности на x. Ако няма такова число, тогава функцията е неограничена.
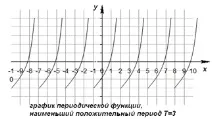
7) Периодичност на функцията.
Функция f(x) е периодична, ако съществува ненулево число T, така че за всяко x от домейна на функцията, f(x+T) = f(x). Това най-малко число се нарича период на функцията. Всички тригонометрични функции са периодични. (Тригонометрични формули).
Функцияf се нарича периодична, ако съществува такова число, че за всякоx от областта на дефиницията е вярно равенствотоf(x)=f(x-T)=f(x+T).T е периодът на функцията.
Всяка периодична функция има безкраен брой периоди. На практика обикновено се взема предвид най-малкият положителен период.
Стойностите на периодичната функция се повтарят след интервал, равен на периода. Това се използва при изчертаване на графики.