Остатък. Основна теорема за остатъка. Прилагане на остатъка за изчисляване на интеграли - решаване на проблеми








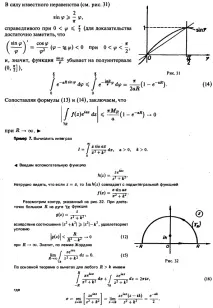





] в разширението на Лоран на тази функция в точката z0. Това означава, по-специално, че остатъкът в отстранима особена точка е равен на нула. Нека посочим някои формули за изчисляване на остатъка на полюса на функцията f(r). 1. zq - полюс от първи ред: 00 Умножаваме двете части на това равенство по z - zo и, преминавайки към границата при z zo, получаваме, че Ако функцията f (z) може да бъде представена като дроб, където и f (z) са аналитични функции, и прост полюс, тогава от формула (3) следва, че Следователно, 2. zo е полюс от порядък m: За да елиминирате отрицателните степени на z - z0, умножете двете страни на това равенство по (z-Zo)m, Остатъци Основната теорема за остатъците Прилагане на остатъци към изчисляване на интеграли Остатък на функция по отношение на точка в безкрайност Приложение на остатъци към изчисляване на определени интеграли Интеграли на рационални функции Лема на Джордан Изчисляване на Fre snel интеграли до границата при получаваме, че Пример 2. Нека 4 Особените точки на тази функция са точките r = ±i. Това са полюси от втори ред. Нека изчислим, например, res/(i). Имаме Теорема 21i. Нека функцията f(z) е аналитична навсякъде в областта D, с изключение на краен брой изолирани сингулярни точки 7, тогава за всяка затворена област G, лежаща в D и съдържаща точки zn вътре, е в сила следното равенство. Теоремата следва от теоремата на Коши за многосвързана област. Нека построим кръгове от такъв малъкс радиус r, че ограничените от тях окръжности се съдържат в областта G и не се пресичат (фиг. 29). Означаваме с G* площта, която се получава от площта G чрез премахване на кръговете U и . U „. Функцията f(z) е аналитична в G* и непрекъсната в своето затваряне G7. Следователно, по теоремата на Коши за многосвързана област, имаме От тази формула, използвайки дефиницията на остатъка, получаваме изискваното равенство (5). 6.1. Остатъкът на функция по отношение на безкрайната точка За функция f(z) се казва, че е аналитична в безкрайната точка z = oo, ако функцията е аналитична в точката C = 0. Това трябва да се разбира по следния начин: функцията g(0 = f(f) може да бъде разширена до аналитична функция, като се зададе, например, функцията е аналитична в точката z = oo, тъй като функцията е аналитична в точката C = 0. Нека функцията f(r) е аналитична в някаква околност на безкрайно отдалечена точка (с изключение на самата точка z = oo). Точката z = oo се нарича изолирана сингулярна точка на функцията f(z) ако в някои околности на тази точка няма други сингулярни точки на функцията f(z). Полюсите zk = k-k на тази функция се натрупват в безкрайност, ако k oo. Казва се, че z - oo е отстранима сингулярна фина точка, полюс или съществена сингулярна точка на функцията f(z), в зависимост от това дали lim f(z) е краен, безкраен или изобщо не съществува. Критериите за типа точка в безкрайността, свързани с Lau промяна на разширението на рентата в сравнение с критериите за крайни сингулярни точки Теорема 22. Ако z - oo е отстранима сингулярна точка на функцията /(z), тогава разширението на Лоран на f(z) в близост до тази точка не съдържа положителни степени на z;z. Разширението на Лоран на функцията /(z) в околност на точка в безкрайност е разширението на Лоран в редица на Лоран, която се събира навсякъде извън окръжност с достатъчно голям радиус R с център в точката z = 0 (с изключение, може би, в самата точка z = oo). Нека функцията f(z) е аналитична в някаква околност на точката z = oo (с изключение може би на самата тази точка). Остатъкът на функцията f(z) в безкрайност е величината pae 7 — достатъчно голяма окръжност \z\ = p, пресечена по посока на часовниковата стрелка (така че околността на точката z - oo остава отляво, както в случая на крайната точка r = r0). И от това определение следва, че остатъкът на функция в безкрайност е равен на коефициента при z
! в разширението на Лоран /(z) в околност на точката z - oo, взета с обратен знак: Пример 3. За функцията f(z) = имаме f(z) = 1 + j. Този израз може да се разглежда като неговото разширение на Лоран в околността на + точки z = oo. Лесно е да се види, че точката z = oo е отстранима особена точка и ние задаваме, както обикновено, /(oo) = 1. Ето защо, от този пример следва, че остатъкът на аналитична функция по отношение на отстранима особена точка в безкрайност (за разлика от крайна отстранима особена точка) може да се окаже, че е различен от нула. Добре познатите разширения на Тейлър на функциите e1, cosz, sinz, chz, shz също могат да се разглеждат като разширения на Лоран в околност на точката z - oo. Тъй като всички тези разширения съдържат безкраен набор от положителни степени на z, изброените функции имат съществена особеност в точката z = oo. Теорема 23. Ако функция f(z) има краен брой особени точки в разширената комплексна равнина, тогава сумата от всички нейни остатъци, включително остатъка в безкрайност, е равна на нула. Така че, ако са крайните сингулярни точки на функцията f 0 е реално число. ПриПри изчисляването на такива интеграли често е полезна следната лема. Джордан Лема. Нека функцията f(z) е аналитична в горната полуравнина, с изключение на краен брой изолирани сингулярни точки, и като \ клони към нула равномерно по отношение на arg z. Тогава, за всяко положително a, където 7n е горният полукръг.Условието, че f(r) клони равномерно към нула, означава, че на полукръга 7R Нека оценим изследвания intefal. Отбелязвайки, че на 7A По силата на добре известното неравенство (виж Фиг. 31), валидно за (за да го докажем, достатъчно е да отбележим, че u, следователно, функцията ^ намалява на полуинтервала. Сравнявайки формули (13) и (14), заключаваме, че , поради връзката Този метод дава възможност да се приложи и в случай, когато функцията f(z) има особени точки (прости полюси) върху реалната ос. Нека покажем как се прави. Пример 8. Изчислете интеграла 4 функцията има следните свойства: за съвпада с подинтегралната функция; 2) има особеност на реалната ос - прост полюс в точката z = 0. Помислете, в горната полуравнина Im z ^ 0, затворен контур Γ, състоящ се от сегменти на реалната ос [-R, -r), (r, R) и дъгиполукръгове (фиг. 33). Вътре в този контур има само един полюс на функцията h(z) - точката z = Ы. Съгласно основната теорема за остатъка, нека първо преобразуваме сумата от интегралите по сегментите (-i, -i и r, i) на реалната ос. Замяна на x с
x в първия член от дясната страна на равенството (18) и го комбинираме с третия член, получаваме Нека се обърнем към втория член във формула (18). Тъй като където lim g(z) = 0. то интеграндът h(z) може да се представи в следния вид: Тогава Настройка . получаваме, че четвъртият член в равенство (18) клони към нула при λ —» оо, съгласно лемата на Джордан, тъй като функцията ^ клони към нула при r oo. Така за , равенството (18) приема формата 6.3. Изчисляване на интегралите на Френел. Интегралите на Френел: Разгледайте спомагателната функция f(r) = c" и контура Γ, показан на Фиг. . Вътре в контура Γ, функцията f(z) е аналитична и чрез теоремата на Коши показваме, че където r2 е полукръг с радиус r2. На интервала BO: Оттук откъде Упражнения Намерете реалните и въображаемите части на функцията: Намерете изображенията на реалната и въображаемата ос, когато се показват: Докажете, че функцията е непрекъсната в цялата комплексна равнина: Използвайки условията на Коши-Риман, разберете дали функцията е аналитична поне в една точка или не: Възстановете функцията f(r), която е аналитична в съседство на точка 20 от известната реална част u (или от известната въображаема част v(x, y)) и стойността на f(z0): Покажете, че следните функции са хармонична: Може ли дадената функция да бъде реална или имагинерна част от аналитична функция Намерете реалната и имагинерната част на функцията: Намерете модула и главната стойност на аргумента на функцията в посочената точка zq:Намерете логаритмите на следните числа: Решете уравнението: 38. Изчислете интеграла / - правата, свързваща точките z\ \u003d 0 отрето с правата, б) дъгата на параболата е начупена 39. Изчислете интеграла - полуокръжността Изчислете интегралите: 43. Изчислете интеграла / където 7 е горната половина на окръжността * "ос z \u003d 1 (избрани остатъци Основната теорема за остатъците Прилагане на остатъци към изчисляване на интеграли Остатък на функция по отношение на точка в безкрайност Приложение на остатъци към изчисляване на определени интеграли Интеграли на рационални функции Лема на Джордан Изчисляване на интеграли на Френел клон на функцията и l / z, за които 44. Изчислете интеграла / ^ dz, където 7 е отсечка от права линия, излизаща от точката zj = 1 до точка Изчислете интегралите: Намерете радиуса на сходимост на редицата: Разгънете функцията в редица на Тейлър и намерете радиуса на сходимост на получената редица: по степени на z + I. 55. cosz по степени на 56.--- по степени на z + 2. 57.-^- по степени на z. 58. sh2 z по степени на z. Намерете нулите на функцията и определете техния ред: z nom ring: Намерете особени точки и определете техния характер: Намерете остатъците на функцията в особени точки: Изчислете интеграли: Определете характера на точка в безкрайност: Изчислете интеграли: Отговори z преминават през оста s, когато z се променя от -oo на + oo и се променя от -oo и от + oo на +1 (точка +1 е изключена), оста y преминава в окръжност Оста x s преминава в оста и по същия начин, както в упражнение 5, оста y става права линия u
1, преминаващ от точка 1 към 1 + също и от 1 -»oo до точка 1 (самата точка 1 е изключена