Относно размитата логика
Здравейте граждани и граждани. По заповед на лявата пета реших да започна поредица от научно-популярни статии, където ще обясня основите на изкуствения интелект. Затова в бъдеще ще се пробвам в ролята на гостуващ лектор, който говори за това как космическите кораби разорават просторите на Болшой театър.
Не мога да публикувам по една статия на ден, така че няма да обещавам нищо, за да не се затруднявам с тези задължения. Единственото нещо: няма да измъчвам другите с изобилие от математика, ще се опитам да изложа всичко възможно най-достъпно, но без ругатни. Ще започна цикъла с апарата на размитата логика, където ще обясня каква е интелектуалността му.
Нека се приближим до тялото, до теорията на размитите множества. Създадена е от американски учен от азербайджански произход Лотфи Заде, за да адаптира теорията на множествата към начина на човешкото мислене. В крайна сметка, как мисли човек? Ако, докато сте на плажа, попитате плувец: „Кажи ми, скъпи човече, каква е температурата на водата по скалата на Фаренхайт, с точност до десета от градуса?“ - той ще ви погледне, сякаш сте психично болен. И ако зададете въпроса: „Как е водата днес?“, Той ще каже: „Студена / гореща / топла“ или ще промърмори „мокра“, ако днес не е в духа. Цялата работа е, че "студена вода" е доста неясна формулировка. Единият ще се грее в блаженство, където другият ще тича до брега, за да се грее след две минути. Така работи човек, субективизъм и липса на ясни граници - това е за нас.
Някои вече са успели да разберат защо са размити множества. Изключително трудно е да се определи колко хора имат свойството "високо". За мен двуметров красив мъж, наклонен фатмън в раменете, висок поне не е по-нисък от нивото на ухото ми. И Шортиедин и половина метра ще гледа човек с височина 170 см с вдигната глава - за него високият растеж започва много по-рано. Тук става дума за субективизъм.
Втората трудност се състои в размиването на границите. Възможно ли е точно да се определи броят на сантиметрите, които ще разделят човек със среден ръст от нисък? 170 и половина? 172 и три четвърти? Разделението е много, много условно. И така, ние се доближихме до разликата между размитите множества и ясните.
Дърлене на барабани, пауза на Мхатов… И така, размитите множества се различават от отчетливите по това, че обектите, принадлежащи към размитите множества, могат да имат свойство, което ги определя в различна степен. Ние се съгласихме да считаме тази степен на членство като лежаща в диапазона от нула до едно, но ако на някого е по-удобно, той може да умножи по 100 и ще получите проценти.
Защо създаването на такава теория беше толкова важно, защо й беше обърнато толкова голямо внимание? Отговорът е прост: тук е скрита златна мина. Огромна широчина на приложение. Да приемем, че сте инженер и задачата ви е да проектирате микровълнова фурна. До каква температура човек ще затопли храната? До 40,2°C? Майната му. До горещ, че има размит набор. А задачата на микровълновата фурна е да даде на мъфина такава температура, която с една степен на сигурност да принадлежи към набора „горещо“.
Тогава започва най-забавното, бягащите от уроците по математика могат да се разпръснат настрани с вой. А? Какво? Обещах ли да се справя без него? Както каза старият Арни в известния филм – „Излъгах“. Степента на членство обикновено се обозначава с гръцката буква "mu" - μ. За да не се отегчаваме, нека въведем понятието лингвистична променлива - това е такава променлива, която може да приеме стойност под формата на думи на човешки език. Тоест лингвистичната променлива "растеж"може да приема стойности: "високо", "средно", "ниско". Стойностите на лингвистичната променлива ще се наричат набори от термини, обръщам внимание на факта, че те са размити. И накрая, има концепцията за универсален набор - обикновен, ясен набор, съдържащ всички стойности, които една обикновена променлива може да приеме. Обичайната променлива "височина на човек" може да приема стойности от нула до "колко има рекорд на Гинес, не помня."
Задачата на функцията за принадлежност (FP) е да определи степента, в която обикновена променлива принадлежи към стойността на лингвистична променлива. Тъй като започнах да педалирам темата за височината, ще развия: FP определя степента, в която човек с височина 184 см принадлежи към „средния“ набор от термини. И така, да заприличаме на бабите. Имаме лингвистична променлива. Имаме няколко негови стойности, всяка от които е размит набор. И накрая, имаме универсален набор - набор от числени стойности на обикновена променлива. Изправени сме пред следната цел: да определим за всяко от размитите множества собствена функция на принадлежност, т.е. за всеки от елементите на универсалното множество посочете степента на членство в съответното размито множество. След това можем да разгледаме конкретна стойност на променливата и да видим до каква степен тя принадлежи към всяко размито множество. Всичко, бурята отмина, можете да изтриете потта и да се отпуснете за известно време. След това ще излязат забавни снимки, след което ще продължим да се забавляваме известно време. В снимките ще илюстрирам значението на функцията на членство, ще покажа какви видове са тези животни, с какво се хранят и ще обясня как да построя тези животни. Да се върнем към любимата ви тема за човешкия растеж. Нека вземем за пример набора "средно" и начертаем графиката на функцията на принадлежност.
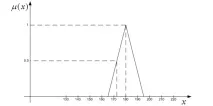
Сега можете, въоръжен рязкос подострен молив изберете произволна стойност на "x" и вижте до каква степен това x удовлетворява условието за среден растеж. Фактът, че осемдесет метра е желязо. Метър седемдесет и два - със степен 0,5. Растежът на метър и петдесет не е среден, така че степента на принадлежност е нула. И така нататък. Обърнете внимание, че намалената функция се нарича триъгълна. Трудно е за вярване, но въпреки това.
Но ние взехме готова функция, която някой (някой!) любезно ни предостави. Как сами да изградите подобна функция? Има два начина: прост и с проблеми. По очевидни причини ще опиша само една проста. Първо, трябва да съберете група от експерти. Е, това са тези безделници, които вярват, че разбират всичко и знаят как всъщност работи светът. Дайте на всеки експерт молив и бележник. След това избройте стойностите на променливата и помолете да поставите "1" (стик, кръстче - по избор) пред тази стойност, ако експертът смята, че стойността на променливата принадлежи към размития набор. Нула - иначе. След това за всяка стойност на променливата сумирайте нулите и единиците и вземете средната стойност - тоест разделете получената сума на броя на безделниците. Получената стойност ще бъде в диапазона от нула до едно (и двете стойности са включени). Някои може да се досетят, че сме получили стойността на функцията за принадлежност за определена стойност на променливата. След като сте получили стойностите на FP за всички стойности на променливата x, можете да изградите графика. Или не строете, ако сте твърде мързеливи.