Параболична форма на тенденция

Експортиране

Резултатите от изчисляването на параметрите на модела на параболичния тренд за експорт са както следва:

Резултатите от изчисляването на параметрите на модела на параболичния тренд за динамичните серии на обема на износа на Китай за периода от 1977 г. до 2012 г.

Нека анализираме полученото уравнение:

Резултати от анализа на дисперсията на модела на параболичната тенденция за времевите редове на обема на износа на Китай за периода от 1977 г. до 2012 г.

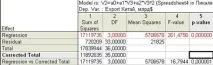
Импортиране

Резултатите от изчисляването на параметрите на модела на параболичния тренд за импортиране са както следва:

Резултатите от изчисляването на параметрите на модела на параболичния тренд за времевия ред на вноса на Китай за периода от 1977 г. до 2012 г.

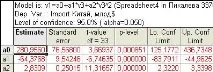
Нека анализираме полученото уравнение:

Резултати от анализа на дисперсията на модела на параболичния тренд за времевите редове на китайския внос за периода от 1977 г. до 2012 г.

След това в таблична форма ще сравним получените данни и ще идентифицираме най-добрия модел на тенденция.

Сравнение на уравненията на тенденциите за времеви редове на износа и вноса на Китай за периода от 1977 до 2012 г.

Експортиране
тренд форма	уравнението	R2	Е
линеен		0,671	69.22
демонстрация		0,989	1246.46
параболичен		0,969	261,48
Импортиране
тренд форма	уравнението	R2	Е
линеен		0,652	63,82
демонстрация		0,994	2073.4
параболичен		0,963	219,54

Следователно най-добрият тренд модел за динамичните редове, както за износа, така и за вноса, ще бъде показателен, т.к съответства на максималните стойности на коефициента на определяне R 2 и F-критерия на Фишер.

По-нататъшният анализ включва изграждането на таблица с наблюдавани и прогнозирани стойности и остатъци на модела на експоненциалната тенденция (Таблици 19, 20).

След това е необходимо да се извърши контрол на качеството на избрания модел.

Най-важният елемент от оценката на качеството на избрания модел е анализът на автокорелацията в остатъците,, т.е. в отклоненията на първоначалните стойности на динамичната серия от тези, изчислени от уравнението на тренда.

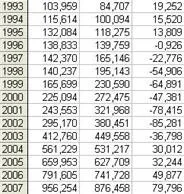
Таблица 19 наблюдавани и прогнозирани стойности и остатъци за модела на експоненциалната тенденция за времеви редове за обема на износа на Китай от 1977 г. до 2012 г.

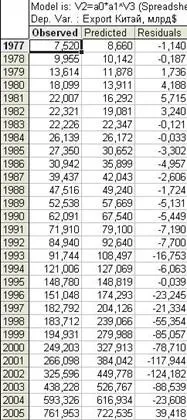
Таблица от 20 наблюдавани и прогнозирани стойности и остатъци за модела на експоненциалната тенденция за времевите редове на обема на вноса на Китай от 1977 г. до 2012 г.

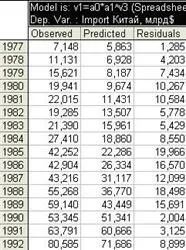
Автокорелацията в остатъците е зависимостта на остатъците от период t от остатъците от предходния период (t-1).

Графично този анализ ще изглежда така:

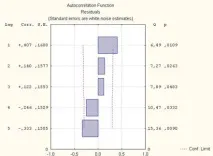
Фигура 2. Графично представяне на автокорелационния анализ в остатъците за времевия ред на обема на износа на Китай за периода от 1977 до 2012 г.

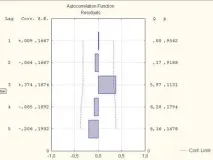
Фигура 3. Графично представяне на автокорелационния анализ в остатъците за времевите редове на обема на вноса на Китай за периода от 1977 до 2012 г.

Автокорелацията се счита за значима, ако , т.е. ако коефициентът на автокорелация в остатъците е статистически значим, то в тяхима тенденция. И тъй като целта на конструирането на уравнението на тенденцията е пълно описание на тенденцията, наличието на автокорелация в остатъците, съответно, показва непълно описание на тенденцията.

Графичното представяне на изчислените коефициенти на автокорелация ясно показва, че те не са статистически значими, тъй като техните стойности не излизат извън границите на доверителните интервали, посочени на графиката с червената пунктирана линия.

В нашия случай автокорелацията в остатъците е незначителна, на базата на която този трендов модел може да се използва за прогнозиране.

Прогнозиране

Един от най-разпространените методи за прогнозиране е екстраполацията, т.е. в разширяването в бъдещето на тенденцията, наблюдавана в миналото.

Екстраполацията се основава на следните предположения:

1) развитието на явлението може разумно да се характеризира с гладка (еволюционна) траектория - тенденция;

2) общите условия, които определят тенденцията на развитие в миналото, няма да претърпят значителни промени в бъдеще.

По този начин екстраполацията дава описание на някакво общо бъдещо развитие на обекта на прогнозиране.

Експортиране

Нека направим прогноза за 2 години въз основа на екстраполацията на най-добрата форма на тренда (индикативен) за времевия ред на износа на Китай за периода от 1977 до 2012 г.:

Тази серия има 36 нива, обозначени с естествени числа. Съответно, прогнозата за обема на износа на Китай през 2013 г. (t=37) и през 2014 г. (t=38) ще бъде:

Импортиране

Нека направим прогноза за 2 години въз основа на екстраполация на най-добрата форма на тренда (индикативен) за времевия ред на вноса на Китай за периода от 1977 до 2012 г.:

Този ред има 36 нива,отбелязани с естествени числа. Съответно прогнозата за обема на китайския внос през 2013 г. (t=37) и през 2014 г. (t=38) ще бъде:

Екстраполацията дава възможност да се получи точкова стойност на прогнозата, която може да се счита за задоволителна само ако има функционална зависимост. Икономическите явления обаче се характеризират с корелационна зависимост, а променливите по правило са непрекъснати. Следователно посочването на точковите стойности на прогнозата, строго погледнато, е лишено от съдържание. От това следва, че прогнозата трябва да се даде като интервал от стойности, т.е. необходимо е да се определи доверителният интервал на прогнозата.

Доверителният интервал отчита само несигурността, свързана с ограничения брой наблюдения и съответната неточност на установените оценки на параметрите на кривата. Основният въпрос - до каква степен откритата тенденция ще продължи в бъдеще - естествено не може да бъде решен с помощта на такива доверителни интервали. Това е въпрос на смислен икономически анализ и експертна оценка.

Най-общо доверителният интервал за тенденция се определя като:

,

където е средната квадратична грешка на тренда; е изчислената стойност на нивото на серията; –стойност наt-статистика на Студент.

Стойността на коефициента на доверие t=4,3 се изчислява на базата на таблиците с резултатите от изчисляването на параметрите на параболичните модели с помощта на калкулатор в програмата Statistica. Стойността на стандартното отклонение Sy може да се определи чрез анализ на дисперсионни таблици.

Експортиране

По този начин доверителният интервал на прогнозата за 2013 г. се определя като:

Тази прогноза може да се тълкува по следния начин: обемът на китайския износ през 2013 г. с вероятност от 95% ще бъде от 2439,74 милиарда долара до2560,26 милиарда долара.

Доверителният интервал на прогнозата за 2014 г. се определя като:

Тази прогноза може да се тълкува по следния начин: обемът на износа на Китай през 2014 г. с 95% вероятност ще бъде от 2864,74 милиарда долара до 2985,26 милиарда долара.

Импортиране

Доверителният интервал на прогнозата за 2013 г. се определя като:

Тази прогноза може да се тълкува по следния начин: обемът на китайския внос през 2013 г. с 95% вероятност ще бъде от 2223,07 милиарда долара до 2307,43 милиарда долара.

Доверителният интервал на прогнозата за 2014 г. се определя като:

Тази прогноза може да се тълкува по следния начин: обемът на китайския внос през 2014 г. с 95% вероятност ще бъде от 2630,82 милиарда долара до 2715,18 милиарда долара.

Според Държавния митнически комитет на Китайската народна република през 2013 г. износът на Китай възлиза на 2210,02 милиарда долара, вносът - 1950,29 милиарда долара.

Следователно реалните обеми на износа и вноса на Китай през 2013 г. в повечето случаи се оказват по-ниски от прогнозираните стойности. Този факт може да е следствие от факта, че трендовият модел не отчита краткосрочните промени в структурата на изследваните процеси. Действителните стойности обаче се оказаха много близки до долната граница на доверителния интервал на прогнозираните стойности според модела на експоненциалната тенденция. И отбелязваме, че би било най-правилно да се разглежда екстраполацията не като краен резултат от прогнозата, а като някаква отправна точка, въз основа на която, с включването на допълнителна информация, която не се съдържа в самата динамична серия, се разработва прогноза.

---