пирамидален сорт
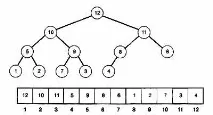
Heapsort се основава на специален тип двоично дърво, наречено heap; стойността на корена във всяко поддърво на такова дърво е по-голяма от стойността на всеки от неговите наследници. Непосредствените деца на всеки възел не са подредени, така че понякога лявото непосредствено дете е по-голямо от дясното, а понякога и обратното. Пирамидата е пълно дърво, в което запълването на ново ниво започва едва след като предишното ниво е напълно запълнено, а всички възли в същото ниво се запълват отляво надясно. Сортирането започва с изграждането на пирамида. В този случай максималният елемент от списъка завършва на върха на дървото: в края на краищата, потомците на върха трябва задължително да са по-малки. След това коренът се записва като последен елемент от списъка и пирамидата с премахнатия максимален елемент се преоформя. В резултат на това вторият по големина елемент е в основата, той се копира в списъка и процедурата се повтаря, докато всички елементи се върнат в списъка. Ето как изглежда съответният алгоритъм: Някои подробности в този алгоритъм трябва да бъдат изяснени. Първо, трябва да определим от какво се състоят процедурите за конструиране и преоформяне на пирамидата: това се отразява на ефективността на алгоритъма. Интересуваме се от реализацията на алгоритъма. Разходите за създаване на двоично дърво нарастват с нарастването на списъка. Можете обаче да използвате мястото, заето от списъка. Възможно е списъкът да се „преустрои“ в пирамида, като се има предвид, че всеки вътрешен възел има две непосредствени деца, с възможното изключение на един възел на предпоследното ниво. Следният дисплей ви позволява да оформите необходимата пирамида. Непосредствените наследници на елемента от списъка с номер i ще бъдат записани на позиции 2i и 2i + 1. Обърнете внимание, че в резултат на това позициите на всички наследници ще бъдатразличен. Знаем, че ако 2i > N, тогава възел i е лист и ако 2i = N, тогава възел i има точно едно дете. Фигурата по-долу показва пирамида и нейното представяне в списък.
Реформиране на пирамидата При копиране на най-големия елемент от корена в списъка, основният възел остава свободен. Знаем, че по-голямото от двете непосредствени деца трябва да попадне в него и трябва да помислим кой ще заеме неговото място и т.н. При това пирамидата трябва да остане възможно най-близо до пълното дърво. Започваме да оформяме пирамидата от най-десния елемент на долното й ниво. В резултат на това възлите от дъното на дървото ще бъдат премахнати равномерно. Ако това не се спазва и всички големи стойности се окажат в една част на пирамидата, тогава пирамидата ще бъде небалансирана и ефективността на алгоритъма ще намалее. Ето резултата: Разглеждайки параметрите на този алгоритъм, може да се чудите защо е необходима коренната променлива. Всъщност, тъй като процедурата не е рекурсивна, коренът на пирамидата винаги трябва да бъде първият елемент. Ще видим обаче, че този допълнителен параметър ще ни позволи да изградим пирамида отдолу нагоре. Стойността на дясната граница е въведена, защото когато елементите се презаписват от пирамидата в списъка, пирамидата се свива.
Изграждане на пирамида Нашият подход към функцията FixHeap ни позволява да формираме първоначалното състояние на пирамидата. Всеки две стойности могат да се считат за листа на свободен възел. Тъй като всички елементи са листа, няма нужда да правите нищо с втората половина на списъка. Можем просто да направим малки пирамиди от листата и след това постепенно да ги изградим заедно, докато всички стойности са в списъка. Следният цикъл ви позволява да приложите тази процедура:Краеналгоритъм Съединявайки написаното и добавяйки необходимите операции за прехвърляне на елементи от пирамидата към списъка, получаваме крайния алгоритъм: