Пиърс стрела
| ИЛИ-НИТО, НИТО |
| Диаграма на Вен |
| x + y ¯ >> |
| ( 1000 ) |
| x ¯ ⋅ y ¯ >\cdot >> |
| x ¯ ⋅ y ¯ >\cdot >> |
| 1 ⊕ x ⊕ y ⊕ x y |
| Не |
| Не |
| Не |
| Не |
| Не |
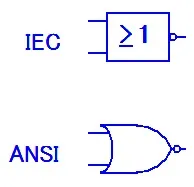
Стрелка на Пиърс(функция на Уеб,отричане на дизюнкция) [1] — двоична логическа операция, булева функция върху две променливи. Въведен от Чарлз Пиърс през 1880-1881 г.
Стрелката на Пиърс, обикновено означавана с ↓, е еквивалентна на операция NOR [2] и се дава от следната таблица на истината:
По този начин твърдението "X ↓ Y" означава "(не X) и (не Y)". Промяната на местата на операндите не променя резултата от операцията.
Стрелката на Пиърс, подобно на чертата на Шефър, формира функционално завършена логическа основа за пространството от булеви функции на две променливи. Това означава, че с помощта само на стрелката на Пиърс е възможно да се конструират всички други логически операции, например:
X ↓ X ≡ ¬ X — отрицание ( X ↓ X ) ↓ ( Y ↓ Y ) ≡ X ∧ Y \right)\downarrow \left(\right)\equiv > — връзка ( X ↓ Y ) ↓ ( X ↓ Y ) ≡ X ∨ Y \right)\downarrow \left(\right)\equiv X\vee Y> — дизюнкция ( ( X ↓ X ) ↓ Y ) ↓ ( ( X ↓ X ) ↓ Y ) ≡ X → Y \right)\downarrow Y\right)\downarrow \left(\left(\right)\downarrow Y\right)\equiv X\rightarrow Y> - внушение
В електрониката това означава, че за прилагане на цялото разнообразие от схеми за преобразуване на сигнали, представящи логически стойности, е достатъчен един типичен елемент, който се нарича „операция 2-ИЛИ-НЕ“ (2-in NOR). От друга страна, този подход увеличава сложността на схемите, които изпълняват изразите и по този начин намалява тяхната надеждност.
Функционална операция, извършена върху n входа, се определя от следния израз:
F \u003d x 1 + x 2 + x 3 + x 4 +. . . x n ¯ . +x_+x_+x_+. x_>>.>
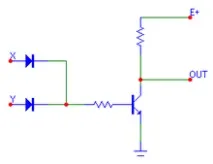
С прости думи, порта 2OR-NOT е 2OR със свързан към него инвертор. За по-голяма яснота по-долу е даден пример за логика 2ИЛИ-НЕ с ключове. Както знаете, логиката 2ИЛИ е близка до израза „Или А, или Б, или и двете“. За да получите логика 2ИЛИ-НЕ, резултатът от 2ИЛИ трябва да бъде обърнат, за да се получи „Не А, Не Б“. На диаграмата по-долу това изглежда така: Превключвателите са маркирани в сиво в състояние "изключено", синьо в състояние "включено". В първата диаграма вляво и двата превключвателя са в изключено положение. По този начин, следвайки изходния израз, получаваме логическа 0. Обърнатият резултат ще бъде равен на 1 и по този начин логически ще удовлетвори израза „Не A, не B“. Следващите диаграми показват съответно „ИЛИ A“, „ИЛИ B“, „И A, И B“, последвано от инверсия на резултата.
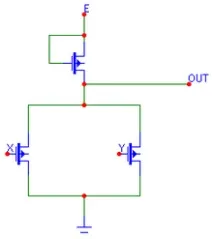
Отляво са опциите за прилагане на порта 2OR-NOT, използвайки диодно-транзисторна логика и съответно MOS.
Представената схема на MOS е направена на същия тип MOS транзистори, но има вариант на схемата 2OR-NOT на допълнителни (допълнителни) MOS транзистори. Такава схема се получава чрез последователно свързване на един и същи тип транзистори и паралелно свързване на група транзисториразличен тип.