Показателната функция, нейните свойства и най-простите показателни неравенства
В този урок ще повторим дефиницията на експоненциална функция, нейните свойства и графики за различни стойности на основата на степента, ще разгледаме решението на най-простите експоненциални неравенства.
Експоненциална функция с основа, по-голяма от единица, техника за решаване на неравенства
Припомнете си свойствата на експоненциална функция с основа, по-голяма от единица.
:
х – аргумент, независима променлива; y – функция, зависима променлива.
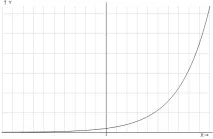
Ориз. 1. Графика на експоненциална функция, основата на степента е по-голяма от единица
Графиката на функцията е експонента (фиг. 1).
Основните свойства на това семейство функции са:
1. Област на дефиниране: .
2. Диапазон от стойности: .
3. Функцията е нарастваща, т.е. по-голяма стойност на аргумента съответства на по-голяма стойност на функцията.
4. Ако аргументът клони към минус безкрайност, функцията клони към нула, ако аргументът клони към плюс безкрайност, функцията също клони към плюс безкрайност.
Монотонното нарастване на функциите от това семейство е ключът към решаването на експоненциални неравенства, при условие че основата на степента е по-голяма от единица.
Метод за решаване на такива неравенства:
1. Изравнете основите на степените.
2. Сравнете показателите, като запазите знака за неравенство.
Експоненциална функция с основа по-малка от единица, техника за решаване на неравенства
Припомнете си свойствата на експоненциална функция с основа по-малка от единица, но по-голяма от нула (фиг. 2).
:
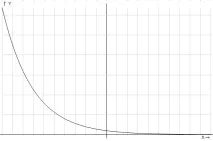
Ориз. 2. Графика на експоненциална функция, основата на степента е по-малка от единица.
Свойства на това семейство функции:
1. Област на дефиниране: .
2. Диапазон от стойности: .
3. Функцията е намаляваща, т.е. по-голямата стойност на аргумента съответства на по-малката стойностфункции.
4. Ако аргументът клони към минус безкрайност, функцията клони към плюс безкрайност, ако аргументът клони към плюс безкрайност, функцията клони към нула.
Монотонното разпадане на функции от това семейство е ключът към решаването на експоненциални неравенства, при условие че основата на степента е по-малка от единица, но по-голяма от нула.
Метод за решаване на такива неравенства:
1. Изравнете основите на степените.
2. Сравнете показателите, като смените знака за неравенство.
Решаване на конкретни примери
Нека коригираме горния метод чрез решаване на конкретни неравенства.
а)
б)
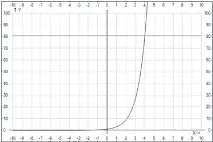
Ориз. 3. Илюстрация за пример 1.b
Графиката на функцията и правата се пресичат в точка с координати (4; 81). Тоест при . По условие трябва да определим кога , това е вярно тогава и само ако .
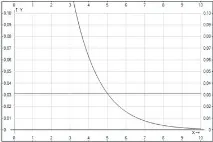
Ориз. 4. Илюстрация за пример 2
Графиката на функцията и правата се пресичат в точка с координати (5; ). Тоест при . По условие трябва да определим кога , това е вярно тогава и само ако .
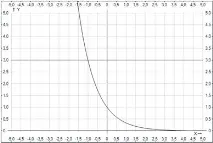
Ориз. 5. Илюстрация за пример 3
Графиката на функцията и правата се пресичат в точка с координати (-1; 3). Тоест при . По условие трябва да определим кога . Това се прави тогава и само ако.
И така, разгледахме решението на най-простите експоненциални неравенства, в следващия урок ще преминем към решаване на експоненциални уравнения.
Препратки
Мордкович А. Г. Алгебра и началото на математическия анализ. – М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и началото на математическия анализ. – М.: Дропла. Колмогоров А. Н., Абрамов А. М., Дудницин Ю. П. и др.. Алгебра и началото на математическия анализ. – М.: Просвещение.
Домашнозадача
Алгебра и началото на анализа, 10–11 клас (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин) 1990 г., № 466,467. Решаване на неравенства:
А) ; б) ; V) ; G) . Решаване на неравенства:
А) ; б) ; V) ; G) .
Допълнителни препоръчителни връзки към интернет ресурси
Математика-повторение. com. Тервър. ru. вашият учител. инфо.