Получаване на синусоидална ЕМП
Основното предимство на синусоидалните токове е, че позволяват най-икономично производство, пренос, разпределение и използване на електрическа енергия. Целесъобразността на тяхното използване се дължи на факта, че ефективността на генераторите, електродвигателите, трансформаторите и електропроводите в този случай е най-висока.
За да се получат синусоидално променящи се токове в линейни вериги, е необходимо напр. д.с. също се променя синусоидално. Помислете за процеса на възникване на синусоидална ЕМП. Най-простият генератор на синусоидална ЕМП може да бъде правоъгълна намотка (рамка), въртяща се равномерно в еднородно магнитно поле с ъглова скорост ω (фиг. 2.1, b).
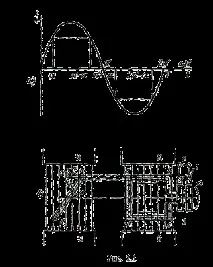
Магнитният поток, проникващ в намотката по време на въртенето на намотката abcd, индуцира (индуцира) в нея въз основа на закона за електромагнитната индукция EMFe. Товарът е свързан към генератора с помощта на четки 1, притиснати към два контактни пръстена 2, които от своя страна са свързани към намотката. Стойността на abcd, индуцирана в намотката e. д.с. във всеки момент от време тя е пропорционална на магнитната индукция B, размера на активната част на намотката l = ab + dc и нормалния компонент на скоростта на нейното движение спрямо полето vn:
където B и l са константи, а vн е променлива, зависеща от ъгъла α. Изразявайки скоростта vn по отношение на линейната скорост на намотката v, получаваме
В израз (2.2) произведението Blv = const. Следователно, e. d.s., индуциран в намотка, въртяща се в магнитно поле, е синусоидална функция на ъгъла α.
Ако ъгълът α = π/2, тогава произведението Blv във формула (2.2) е максимумът (амплитудата)стойността на индуцираната e. д.с. Ем = Бул. Следователно израз (2.2) може да се запише като
Тъй като α е ъгълът на въртене за време t, тогава, изразявайки го чрез ъгловата скорост ω, можем да запишем α = ωt и формула (2.3) може да бъде пренаписана като
където e е моментната стойност на e. д.с. в намотка; α = ωt - фаза, характеризираща стойността на e. д.с. в този момент от време.
Трябва да се отбележи, че моментът д.с. за безкрайно малък период от време може да се счита за постоянна стойност, следователно, за моментни стойности на e. д.с. e, напрежения и токове i, законите на постоянния ток са валидни.
Синусоидалните величини могат да бъдат представени графично чрез синусоиди и въртящи се вектори. Когато са изобразени като синусоиди на ординатата, в определена скала, моментните стойности на количествата са отделени, а времето е на абсцисата. Ако синусоидалната стойност е представена чрез въртящи се вектори, тогава дължината на вектора на скалата отразява амплитудата на синусоидата, ъгълът, образуван с положителната посока на абсцисната ос в началния момент от времето, е равен на началната фаза, а скоростта на въртене на вектора е равна на ъгловата честота. Моментните стойности на синусоидалните величини са проекциите на въртящия се вектор върху оста y. Трябва да се отбележи, че положителната посока на въртене на радиус вектора се счита за посока на въртене обратно на часовниковата стрелка. На фиг. 2.2 са построени графики на моментни стойности на e. д.с. д и д'.
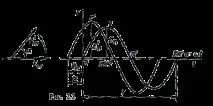
Ако броят на двойките полюси на магнитите е p ≠ 1, тогава за един оборот на намотката (виж фиг. 2.1) има p пълни цикъла на промяна на e. д.с. Ако ъгловата честота на бобината (ротора) е n оборота в минута, тогава периодът ще намалее с pn пъти. Тогава честотата e. d.s., т.е. броя на периодите в секунда,
От фиг. 2.2 се вижда, че ωТ = 2π, откъдето
ω = 2π / T = 2πf (2.5)
стойносттаω, пропорционална на честотата f и равна на ъгловата скорост на въртене на радиус вектора, се нарича ъглова честота. Ъгловата честота се изразява в радиани за секунда (rad/s) или 1/s.
Графично изобразен на фиг. 2.2 д. д.с. e и e' могат да бъдат описани с изразите
Тук ωt и ωt + ψe' са фазите, характеризиращи стойностите на e. д.с. e и e' в даден момент от време; ψe' - началната фаза, която определя стойността на e. д.с. e' при t = 0. За e. д.с. e, началната фаза е равна на нула (ψe = 0). Ъгълът ψ винаги се брои от нулевата стойност на синусоидалната стойност, когато преминава от отрицателни към положителни стойности до началото (t = 0). В този случай положителната начална фаза ψ (фиг. 2.2) се поставя вляво от началото на координатите (към отрицателните стойности на ωt), а отрицателната фаза вдясно.
Ако две или повече синусоидални величини, които се променят с еднаква честота, не съвпадат във времето с началото на синусоидите, тогава те са фазово изместени една спрямо друга, тоест са извън фаза.
Разликата в ъглите φ, равна на разликата в началните фази, се нарича ъгъл на фазово изместване. Фазово отместване между синусоидални величини със същото име, например между две e. д.с. или два тока, означават α. Фазовият ъгъл между синусоидите на тока и напрежението или техните максимални вектори се обозначава с буквата φ (фиг. 2.3).
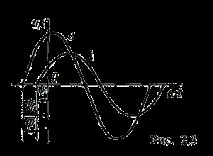
Когато фазовата разлика за синусоидални величини е ±π, тогава те са противоположни по фаза, но ако фазовата разлика е ±π/2, тогава се казва, че са в квадратура. Ако за синусоидални величини с еднаква честота началните фази са еднакви, то това означава, че те са във фаза.
Синусоидално напрежение и ток, чиито графики са показани на фиг. 2.3 са описани, както следва:
освен това фазовият ъгъл между тока инапрежение (виж фиг. 2.3) в този случай φ = ψu - ψi.
Уравнения (2.6) могат да бъдат записани по различен начин:
От тези изрази следва, че напрежението води тока във фаза с ъгъл φ (или токът изостава от напрежението във фаза с ъгъл φ).