Помощни алгоритми с аргументи
Спомнете си темата за помощните алгоритми - за да начертаем два квадрата с различни страни, например 2 и 3, трябваше да напишем два различни помощни алгоритма. Но какво ще стане, ако трябва да нарисувате много различни квадрати с различна дължина на страните? Не пишете свой собствен алгоритъм за всеки! Оказва се, че алгоритмите могат да имат аргументи, възможно е да се състави алгоритъм за начертаване на квадрат с произволна дължина на страната.
Вече се запознахте с понятието аргумент в математиката. В математиката аргументът на функцията е независима променлива, чиито стойности определят стойностите на функцията. Например функцията f(x) = x 2 +1 има един аргумент. За различни стойности на аргумента ще получим различни стойности на функцията - за x=2 получаваме f(x)=5, за x=3 получаваме f(x)=10 и т.н.
Необходимият спомагателен алгоритъм (който чертае квадрат с определена дължина) може да бъде написан по следния начин:
alg square( arg real) начало . долна писалка . преминете към вектора (0, a) . преминете към вектора (a,0) . преместете към вектора (0,-a) . преместете към вектора (-а,0) . повдигане на писалка кон
Нотацията „alg square( arg real a)“ означава, че алгоритъмът „square“ има един аргумент (arg) „a“, който може да бъде произволно реално (реално) число. За да извикате този алгоритъм, трябва да напишете например "квадрат (2)" - получаваме квадрат със страна 2 или "квадрат (3)" - получаваме квадрат със страна 3 и т.н. Някаква специфична стойност "а" ще получи само по време на програмата по време на съответния спомагателен алгоритъм. И навсякъде вместо "а" това число ще бъде заменено с компютъра.
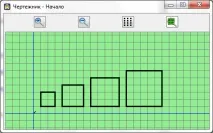
Програмата за рисуване на тази картина може да бъде така:
използвайте Drawer alg squares begin . преминете към точка (1,1) . квадрат (2) .преминете към точка (4,1) . квадрат (3) . преминете към точка (8,1) . квадрат (4) . преминете към точка (13,1) . квадрат (5) . преместване до точка (0,0) край alg square( arg real) начало . долна писалка . преминете към вектора (0, a) . преминете към вектора (a,0) . преместете към вектора (0,-a) . преместете към вектора (-а,0) . повдигане на писалка кон
Нека научим чертожника на нови команди. Нека една от командите се нарича "line(arg th x1,y1,x2,y2)", за да начертаете линия от точка (x1,y1) до точка (x2,y2).
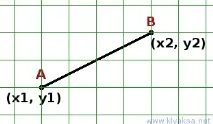
Помощен алгоритъм може да изглежда така:
alg линия (arg елемент x1, y1, x2, y2) начало . преместване до точка (x1,y1) . долна писалка . преместване до точка (x2,y2) . повдигане на писалка кон
Нека втората команда се нарича "rectangle(arg x1,y1,x2,y2)", за да начертаете правоъгълник. Точката (x1,y1) е една точка от AC диагонала на правоъгълника, точката (x2,y2) е срещуположната. Преди да напишете алгоритъма, трябва да разберете какви са координатите на другите две точки.

Помощен алгоритъм може да бъде:
alg правоъгълник (arg x1, y1, x2, y2) начало . преместване до точка (x1,y1) . долна писалка . преместване до точка (x2,y1) . преместване до точка (x2,y2) . преместване до точка (x1,y2) . преместване до точка (x1,y1) . повдигане на писалка кон
Сега с помощта на тези команди ще начертаем къща:
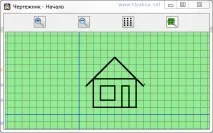
използвайте Draftsman alg house начало . правоъгълник(2,1,8,5) . правоъгълник(3,2,5,4) . правоъгълник (6,1,7,4) . ред(1,4,5,8) . линия(5,8,9,4) край алг линия( арг x1, y1, x2, y2) начало . преместване до точка (x1,y1) . долна писалка . преместване до точка (x2,y2) . повдигнете писалка con alg правоъгълник( arg instx1, y1, x2, y2) старт . преместване до точка (x1,y1) . долна писалка . преместване до точка (x2,y1) . преместване до точка (x2,y2) . преместване до точка (x1,y2) . преместване до точка (x1,y1) . вдигнете писалка con
Забележка: разбира се, заедно с тези команди, можем да използваме стандартните команди на чертожника (преместване в точка, преместване във вектор ...).
Задача 1. Използвайки алгоритмите за помощна линия и правоъгълник, създайте чертеж.
Задача 2. Опитайте се да пренапишете алгоритмите за линия и правоъгълник, така че чертането да се извършва от командата shift vector.
Задача 3. Напишете алгоритъм "правоъгълник (arg w x, y, a, b)", който чертае правоъгълник с дължини на страните a и b, започващ от и завършващ в точката (x, y).
Задача 4. Начертайте сами това, което чертожникът ще нарисува, като изпълните алгоритъма:
използвайте Drawer alg spiral begin . преминете към точка (3,3) . долна писалка . намотка (1); намотка (3); намотка (5); намотка (7); бобина (9) . повдигане на писалка край alg turn( arg inst) начало . преминете към вектора (a, 0) . преместете към вектора (0, -a) . преместване към вектора (-a-1,0) . изместване по вектор (0, a+1) con