Построяване на хистограма и полигон

КУРСОВА РАБОТА

Методи за изследване и моделиране на информационни процеси и технологии

Вариант #6

"Обработка на експериментални данни и оценка на параметрите на разпределението"

студент гр. ISM-51z

СЪДЪРЖАНИЕ

1. ПЪРВИЧНА ОБРАБОТКА НА СТАТИСТИЧЕСКИ………………………………. 3

1.1 Изграждане на интервален статистически ред……………………..……. 3

1.2 Изграждане на хистограма и многоъгълник……………………………………………. 4

Получаване на точкови характеристики. Построяване на теоретична крива……. 5

Конструиране на емпирична функция на разпределение……………………………………..7

2. СТАТИСТИЧЕСКА ИСТИНСКА ПРОВЕРКА НА РАЗШИРЕНАТА НУЛА

2.1 Проверка на истинността на хипотезата H0 чрез критерия на Пиърсън…………………. 8

2.2 Проверка на истинността на хипотезата H0 чрез критерия на Колмогоров……………. 9

3. ИНТЕРВАЛИ ЗА ОЦЕНКА НА ПАРАМЕТРИ НА РАЗПРЕДЕЛЕНИЕТО……………. единадесет

3.1 Доверителен интервал за математическо очакване……………………. единадесет

3.2 Доверителен интервал за стандартно отклонение………. 12

БИБЛИОГРАФИЯ…………………………………. 13

ПРИЛОЖЕНИЕ A. Статистическа таблица……………………………………………………………………14

ИЗЧИСЛЕНИ ДАННИ

опция #6

РАБОТА

Според извлечената случайна извадка (изчислени данни, опция № 6) обща непрекъсната случайна променливаX:

1. направете групирана (интервална) серия на разпределение;

2. конструирайте емпирична функция на разпределение, нейната графика и кумулирайте;

3. изчисляване на емпирични плътности на разпределение, изграждане на хистограма и многоъгълник;

4. получаване на точкови статистически оценки на параметрите на разпределението;

5. конструирайте теоретична крива и изложете хипотеза за закона общо разпространение.

ПЪРВИЧНА ОБРАБОТКА НА СТАТИСТИКА

Изграждане на интервална статистическа серия

Фигура 1 - Първична обработка на експериментални данни

В прозореца на приложението (Фигура 1) се задават и изчисляват следните:

•x– вектор на семплирани стойности.

•n– размер на извадката;

•l– брой интервали;

• min(x) – минимална стойност на извадката;

• max(x)–максимална стойност на извадката;

•h– интервална дължина на интервалната серия;

• f–е матрица, чиято първа колона е средата на интервали от интервалната серия, а втората колона е броят на примерните стойности във всеки интервал.

При изчисляване на променливатаlсе използва вградената функция trunc(z) - цялата част от числотоz, При изчисляване на минималния и максималния елемент на извадката се използват функциите min(x) и max(x), къдетоxе векторът на извадковите стойности. Статистическата функция histogramm(l,x), къдетоlе броят на биновете иxе вектор от извадкови стойности, изчислява средните точки на биновете на статистическата серия (1 колона) и броя на извадковите стойности за всеки бин (2-ра колона) от интервалната серия.

Изграждане на хистограма и многоъгълник

В списъка на Фигура 1 честотният векторp, се изчислява по формулатаp= , , в която броят на примерните стойности за всеки интервалniсе получава чрез избиране на втората колона в матрицата f чрез въвеждане на съответния индекс от панела на матрицата с бутонаM. Векторът fl е векторът на емпиричните плътности, който се изчислява по формулатаf l= .

Фигура 2 показва изчисляването на границите исредата на интервалите. Векторът int е векторът на средните точки на интервала, получен от матрицата f чрез избиране на първата колона в нея чрез въвеждане на съответния индекс от панела на матрицата с бутонаM. Векторът int1 е векторът на границите на интервалите, получен от средата на интервалите чрез изместване на наляво. Последният елемент от колоната int1 е максималният елемент на селекцията.

Фигура 2 - Изчисляване на средните точки и границите на интервалите

След това се изграждат хистограма и многоъгълник.

Фигура 3 - Многоъгълник и хистограма

Получаване на точкови характеристики. Изграждане на теоретична крива

Точковите характеристики (примерни моменти) се изчисляват с помощта на вградени функции:

• средно (x) – извадково средноx;

• медиана (x) – извадкова медиана μ* ;

• Var (x) – коригирана дисперсия на извадкатаs2 ;

• Stdev (x) – коригирано стандартно отклонение на извадката;

• kurt (x) – примерен ексцесE* ;

• Skev (x) – селективна асиметрияA* ;

•x– вектор на семплирани стойности.

Изчисляването на примерните моменти е дадено на фигура 4.

Достатъчно малки стойности на коефициентите на ексцес и асиметрия , както и построената хистограма и многоъгълник ни позволяват да приемем, че общото разпределение е нормално. Следователно, в средата на интервалната серия, стойностите на плътността на нормалното разпределение (вектор f) се изчисляват с помощта на вградената функция dnorm(int,a,σ), където изчислената средна стойност на извадката и стандартното отклонение на извадката се приемат като параметриaи σ.

Фигура 4 - Изчисляване на точкови характеристики и изчисляване на хипотетични плътности на разпределение

НикойФигура 5 показва хистограма и теоретична крива - плътността на нормалното разпределение.

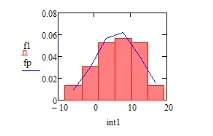
Фигура 5 - Хистограма и теоретична крива

Когато чертаете две функции в един шаблон, трябва да въведете името на една функция (fl) в квадрат вертикално, да натиснете запетая на клавиатурата, и след това да въведете името на втората функция (fp).

---