ПОЗНАЙ ИНТУИТА, Лекция, Балансирани дървета
Спускане по 2-3-4 дървета
Въпреки гаранцията за производителност, предоставена от рандомизирани и изкривени BST, и в двата случая е възможно времето за изпълнение на една операция за търсене да бъде линейно. Следователно тези методи не помагат да се отговори на основния въпрос за балансираните дървета: Има ли тип BST дърво, за което е възможно да се гарантира, че времето за изпълнение на всяка операция за вмъкване и намиране зависи логаритмично от размера на дървото? В този и следващия раздел ще разгледаме абстрактно обобщение на BST и тяхното абстрактно представяне като BST дървовиден тип, което ни позволява да отговорим положително на този въпрос.
За да се гарантира, че създадените BST са балансирани, използваните дървовидни структури трябва да имат известна гъвкавост. За да получим тази гъвкавост, нека приемем, че възлите в нашите дървета могат да съдържат повече от един ключ. А именно, допускаме съществуването на 3-възли и 4-възли, които могат да съдържат съответно два и три ключа. 3-възел съдържа три връзки: една към всички елементи, чиито ключове са по-малки от двата му ключа, една към всички елементи, чиито ключове са между двата му ключа, и една към всички елементи, чиито ключове са по-големи от двата му ключа. По същия начин, 4-възел има четири връзки: по една за всеки от интервалите, дефинирани от неговите три ключа. Тогава възлите в стандартно BST дърво могат да се нарекат 2-възли: те съдържат един ключ и две връзки. По-късно ще разгледаме ефективни начини за дефиниране и прилагане на основни операции върху тези разширени възли; засега ще приемем, че има удобни начини за работа с тях и ще видим как ни позволяват да формираме дървета.
Дефиниция 13.2.Балансираното дърво за търсене 2-3-4 е дърво за търсене 2-3-4, в което всички препратки към празни дървета са на едно и също разстояние от корена.
В тази глава терминът дърво 2-3-4 ще бъде приложен към балансирани дървета за търсене 2-3-4 (в друг контекст това означава по-обща структура). Пример за дърво 2-3-4 е показано на фиг. 13.10.
Алгоритъмът за търсене на ключове в такова дърво е обобщение на алгоритъма за търсене на BST дървета. За да разберем дали има ключ в дървото, сравняваме го с ключовете в корена: ако е равен на някой от тях, търсенето е успешно; в противен случай следваме връзката от корена към поддървото, съответстващо на набора от ключови стойности, към които принадлежи търсеният ключ, и след това рекурсивно извършваме търсене в това дърво. Има няколко начина за представяне на 2-, 3- и 4-възли и търсене на съответната връзка; ние ще отложим тези решения за Раздел 13.4, където ще бъде обсъдено много удобно решение.
За да вмъкнете нов възел в дърво 2-3-4, човек може, както при BST дървета, да извърши неуспешно търсене и след това да се присъедини към възела, но в този случай новото дърво ще бъде небалансирано. Основната причина, поради която 2-3-4 дървета са важни, е, че те ви позволяват да извършвате вмъквания, като същевременно винаги поддържате дървото перфектно балансирано. Например, лесно е да видите какво да правите, ако търсенето завърши на 2 възела: просто го преобразувайте в 3 възела. По същия начин, ако търсенето завърши на 3-възел, достатъчно е да го преобразувате в 4-възел. Но какво ще стане, ако търсенето бъде прекъснато при 4-възела? Решението е, че човек може да намери място за новия ключ, като същевременно поддържа дървото балансирано, като първо раздели 4-възела на два 2-възела и след това предаде средния възел нагоре към родителския възел. Тези три описани случая са показани на фиг.13.11.
Но какво ще стане, ако трябва да разделите 4-възел, чийто родителски възел също е 4-възел? Едно възможно решение би било да се раздели и родителският възел, но предшестващият възел също може да бъде 4-възел и т.н. — може да се наложи да разделите възлите по целия път нагоре в дървото. По-опростен подход е да се гарантира, че пътят на търсене не завършва на 4-възел, като се разбива всеки 4-възел, който срещне, докато се движи надолу по дървото.
Когато слизаме по дървото, не е нужно изрично да се тревожим, че родителят на текущия възел е 4-възел, тъй като трансформациите, които извършваме, гарантират, че докато преминаваме през всеки възел в дървото, ще стигнем до възел, който не е дъщерен на 4-възела. По-специално, когато стигнем до дъното на дървото, ние не сме в 4-възел и можем да вмъкнем нов възел чрез директно преобразуване на 2-възел в 3-възел или 3-възел в 4-възел. Вмъкването може да се разглежда като разделяне на въображаем 4-възел в долната част на дървото, предаване на нов ключ.
Още един нюанс: когато коренът на дървото стане 4-възел, ние просто го разделяме, трансформирайки го в триъгълник, състоящ се от три 2-възела, както за първия разделен възел в предишния пример. Разделянето на корена след вмъкване е малко по-удобно от изчакването на следващото вмъкване, за да извърши разделянето, защото в този случай не е нужно да се грижите за родителския възел на корена. Разделянето на корена (и само тази операция) увеличава височината на дървото с едно ниво.
Тази фигура показва дърво 2-3-4, съдържащо ключовете A S R C H I N G E X M P L .
В такова дърво може да се намери ключ, като се използват ключовете в основния възел, за да се намери връзка към желаното поддърво и след това да се продължи търсенето рекурсивно. Например, за да търсите ключа P в това дърво, трябва да следвате правилната връзка от корена,тъй като P е по-голямо от I, следвайте средната връзка от десния дъщерен възел на корена, тъй като P е между N и R, и накрая завършете успешно търсене в 2-възела, съдържащ ключ P.
2-3-4 дърво само с 2 възела, подобно на BST дърво (отгоре). Ключът C може да бъде вмъкнат чрез преобразуване на 2-възел, при който търсенето на C прекъсва, в 3-възел (втори от горната снимка). По подобен начин човек може да вмъкне ключа H чрез трансформиране на 3-възела, при който търсенето е прекъснато, в 4-възел (третата фигура отгоре). Но вмъкването на ключа I е по-трудно, защото търсенето му е прекъснато в 4-възела. Разделяме 4-възела, предаваме неговия среден ключ на родителския възел и трансформираме този възел в 3-възел (четвъртата кутия отгоре). Тази трансформация създава валидно дърво 2-3-4 с място за I в долната част. И накрая, вмъкваме I в 2-възела, където търсенето сега прекъсва, и трансформираме този възел в 3-възел (долната снимка).
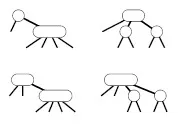
В 2-3-4-дърво всеки 4-възел, който не е дъщерен на 4-възел, може да бъде разделен на два 2-възела чрез предаване на средния му вход към родителския възел. 2-възел с дете с 4 възела (горе вляво) се превръща в 3-възел с две деца с 2 възела (горе вдясно), а 3-възел с дете с 4 възела (долу вляво) става 4-възел с две деца с 2 възела (долу вдясно).
Това показва резултата от вмъкване на елементи с ключове A S E R C H I N G X в първоначално празно дърво 2-3-4. Всеки 4 възела, срещнат по пътя на търсене, се разделя, осигурявайки свободно място за нов елемент в долната част на дървото.
На фиг. Фигура 13.13 показва конструкцията на дърво 2-3-4 чрез последователно вмъкване на набор от ключове. За разлика от стандартните BST дървета, които растат надолу от върха, тези дървета растат отдолу нагоре. Тъй като 4-възела се разделят напът отгоре надолу, такива дървета се наричат низходящи 2-3-4-дървета. Този алгоритъм е важен, защото създава почти идеално балансирани дървета за търсене, въпреки че се извършват само няколко локални трансформации, докато пресича дървото.
Лема 13.6.При търсене в 2-3-4-дървета от N възли се посещават най-много lgN+1 възли.
Всеки външен възел е на същото разстояние от корена: извършените трансформации нямат ефект върху разстоянието между който и да е възел и корена, освен когато коренът е разделен, в който случай разстоянието между всички възли и корена се увеличава с 1. Ако всички възли са 2-възли, горното твърдение е вярно, тъй като такова дърво е подобно на пълно двоично дърво; ако в дървото има 3 и 4 възли, височината може да бъде само по-малка.
Лема 13.7.Вмъкванията в 2-3-4-дървета от N възли изискват по-малко от lg N + 1 разделяне на възел в най-лошия случай и най-вероятно по-малко от един разделяне на възел средно.
В най-лошия случай всички възли по пътя до точката на вмъкване са 4-възли и всичко ще трябва да бъде разделено. Но в дърво, конструирано от произволна пермутация на N елемента, не само че този най-лош случай е малко вероятен, но средно е вероятно да са необходими много малко операции за разделяне, тъй като 4-възлите не са толкова често срещани в дърветата. Например в голямото дърво на фиг. 13.14 фиг. 13.14 всички 4 възела, с изключение на два, са разположени на долното ниво. Досега експертите не са успели да анализират аналитично точно работата на 2-3-4 дървета, но емпирично получените резултати показват, че много малко дялове се използват за балансиране на дървета. Най-лошият случай е само lg N, а в практически ситуации дори той е непостижим.
Горното описание е достатъчно, за да се дефинира алгоритъм за търсене, използващ 2-3-4 дървета, който гарантира достатъчно висока производителност в най-лошия случай. Ние обаче сме само на половината път към изпълнението. Възможно е да се напишат алгоритми, които действително извършват трансформации на различни типове данни, представляващи 2-, 3- и 4-възли, но при повечето от срещаните проблеми прилагането на такова директно представяне не е много удобно. Както при изкривяването на BST, допълнителните разходи за обработка на по-сложни възли могат да направят алгоритмите по-бавни от стандартните BST търсения. Основната цел на балансирането е да предпази от най-лошия случай, но бих искал разходите, свързани с това, да са ниски и да няма допълнителни разходи всеки път, когато алгоритъмът се изпълнява. За щастие, както ще бъде показано в раздел 13.4, има доста просто представяне с 2, 3 и 4 възла, което позволява трансформациите да се извършват по същия начин с малко допълнителни разходи в сравнение със стандартното търсене в двоично дърво.
Това дърво 2-3-4 е резултат от 200 произволни вмъквания в първоначално празното дърво. Всички пътища за търсене в дървото съдържат не повече от шест възела.
Описаният алгоритъм е само един от възможните начини за поддържане на баланс в 2-3-4 дървета за търсене. Разработени са няколко други метода за постигане на същите резултати.
Например можете да балансирате отдолу нагоре. Първо в дървото се търси възелът, разположен в долната част на дървото, към който трябва да принадлежи елементът, който трябва да се вмъкне. Ако този възел е 2-възел или 3-възел, той се преобразува в 3-възел или 4-възел, както е описано по-рано. Ако е 4-възел, той се разделя както преди (с вмъкнат нов елементв един от получените 2-възела в долната част), а средният елемент се вмъква в родителския възел, ако е 2- или 3-възел. Ако родителският възел е 4-възел, той също се разделя (с вмъкване на средния възел от долното ниво в съответния 2-възел) и средният елемент се вмъква в своя родителски възел, ако е 2- или 3-възел. Ако основният възел също е 4-възел, ние продължаваме това изкачване, като разделяме 4-те възела, докато 2-възел или 3-възел се срещне в пътя на търсене.
Този вид балансиране отдолу нагоре може да се направи на дървета, които съдържат само 2- или 3-възела (и не 4-възела). Този подход води до повече операции за разделяне на възли по време на изпълнението на алгоритъма, но е по-лесен за програмиране, тъй като има по-малко случаи за разглеждане. Друг подход намалява броя на разделянията на възли, като търси братя и сестри, които не са с 4 възела, преди да раздели 4-възел.
Както ще бъде показано в раздел 13.4, имплементациите на всички тези методи се основават на една и съща рекурсивна схема. В "Външно търсене" ще бъдат разгледани и обобщенията на тези методи. Основното предимство на разглеждания подход отгоре надолу в сравнение с други методи е, че необходимият баланс може да бъде постигнат в резултат на еднократно преминаване през дървото надолу.
13.39. Начертайте балансирано дърво за търсене 2-3-4, образувано от низходящи вмъквания на елементи с ключове ЛЕСЕН ВЪПРОС в този ред в първоначално празно дърво.
13.40 часа. Начертайте балансирано дърво за търсене 2-3-4, образувано от възходящи вмъквания на елементи с ключове ЛЕСНО ВЪПРОС в този ред в първоначално празно дърво.
13.41. Каква е минималната и максималната възможна височинабалансирани 2-3-4 дървета, съдържащи N възли?
13.42. Каква е минималната и максималната възможна височина на балансирани 2-3-4 двоични дървета за търсене, съдържащи N възли?
13.43. Начертайте всички структурно различни балансирани 2-3-4 двоични дървета за търсене, съдържащи N ключа за .
13.44. Намерете вероятността всяко от дърветата, начертани в упражнение 13.43, да е резултат от вмъкване на N произволни различни елемента в първоначално празното дърво.
13.45 ч. Направете таблица, съдържаща броя на изоморфните дървета от Упражнение 13.43 за всяка стойност на N, в смисъл, че те могат да бъдат трансформирани от едно в друго чрез размяна на поддървета във възли.
13.46. Опишете алгоритми за търсене и вмъкване за балансирани дървета за търсене 2-3-4-5-6.