Преминаване на частици през потенциална бариера
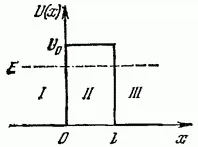
Нека частица, движеща се отляво надясно, срещне по пътя си потенциална бариера с височина и ширина. Според класическите представи поведението на частицата има следния характер. Ако енергията на частицата е по-голяма от височината на бариерата, частицата преминава през бариерата безпрепятствено (на участъка скоростта на частицата само намалява, но след това отново приема първоначалната си стойност) Ако E е по-малко (както е показано на фигурата), тогава частицата се отразява от бариерата и лети в обратна посока; частицата не може да проникне през бариерата.
Поведението на една частица според квантовата механика изглежда съвсем различно. Първо, дори при , има различна от нула вероятност частицата да се отрази от бариерата и да лети в обратната посока. Второ, при E има ненулева вероятност частицата да проникне "през" бариерата и да попадне в областта, където. Такова поведение на микрочастица, което е напълно невъзможно от класическа гледна точка, следва директно от уравнението на Шрьодингер.
Да разгледаме случая. В този случай уравнението има формата
за райони I и III и
за район II, и
Ще търсим решение на уравнение (26.1) във вида (виж § 52 от 1 том). Заместването на тази функция в (26.1) води до характеристичното уравнение:
Така общото решение на уравнение (26.1) има формата
След като решихме уравнение (26.2) чрез заместване, получаваме общото решение на това уравнение във формата
Обърнете внимание, че решението на tzid съответства на вълна, разпространяваща се в положителната посока на оста, докато решението на формата съответства на вълна, разпространяваща се в обратната посока. За да разберем това, припомняме, че обикновена (звукова, електромагнитна и т.н.) плоска вълна, разпространяваща се в посока на нарастване, се описва от реалната част на израза вълна,разпространяваща се в посока на намаляване - реалната част на израза Частица, движеща се в положителна посока на оста, е свързана с функция (виж формула (21.6)). Ако отхвърлим фактора време в тази функция, тогава получаваме израза За частица, движеща се в обратна посока, получаваме
В област III има само вълна, която е преминала през бариерата и се разпространява отляво надясно. Следователно коефициентът в израз (26.4) за трябва да бъде равен на нула. За да намерим останалите коефициенти, използваме условията, на които трябва да отговаря функцията.За да бъде тя непрекъсната в целия диапазон на x от до, трябва да са изпълнени следните условия:
Разделяме всички уравнения на и въвеждаме нотацията:
Тогава уравненията (26.7) приемат формата
Съотношението на квадратите на абсолютните амплитуди на отразената и падащата вълна
определя вероятността за отражение на частица от потенциална бариера и може да се нарече коефициент на отражение.
Съотношението на квадратите на абсолютните амплитуди на предаваните и падащите вълни
определя вероятността частица да премине през бариера и може да се нарече коефициент на предаване (или коефициент на прозрачност).
Ще се интересуваме само от преминаването на частици през бариерата и ще се ограничим до намирането на стойността на D. Вярно е, че след намирането на D е лесно да се намери R, тъй като тези коефициенти са свързани с очевидната връзка:
Умножаваме първото от уравненията (26.9) по i и го добавяме към третото. В резултат на това получаваме:
Сега умножаваме второто от уравненията (26.9) по i и го изваждаме от четвъртото. Получаваме:
Решавайки заедно уравнения (26.11) и (26.12), намираме това
Накрая заместване на намеренотокато използваме стойностите във второто от уравненията (26.9), получаваме израз за:
обикновено е много по-голямо от единица. Следователно в знаменателя на израза членът, съдържащ фактора, може да бъде пренебрегнат в сравнение с члена, съдържащ фактора (комплексни числа и имат еднакъв модул). Така че, можем да поставим
Съгласно (26.10), квадратът на модула на това количество дава вероятността частицата да премине през потенциалната бариера. Имайки предвид какво получаваме:
Изразът има стойност от порядъка на единица. Следователно може да се счита, че
От нашия израз следва, че вероятността една частица да премине през потенциална бариера силно зависи от ширината на бариерата l и от нейния излишък над E, т.е. Ако за определена ширина на бариерата коефициентът на предаване D е, да речем, 0,01, тогава с двукратно увеличение на ширината D става равен, т.е. намалява с фактор 100. Същият ефект в този случай ще бъде причинен от четирикратно увеличение на стойността на . Коефициентът на предаване рязко намалява с увеличаване на масата на частиците.
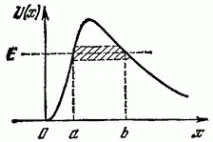
Съответното изчисление показва, че в случай на потенциална бариера на произволна ферма (фиг. 26.2), формулата (26.13) трябва да бъде заменена с по-обща формула:
Когато преодолява потенциална бариера, частицата сякаш преминава през „тунел“ в тази бариера (вижте защрихованата област на фиг. 26.2), във връзка с което явлението, което разгледахме, се нарича тунелен ефект.
От класическа гледна точка ефектът на тунела изглежда абсурден, тъй като частица, „разположена в тунел“, трябва да има отрицателна кинетична енергия (в тунел). Тунелният ефект обаче е специфично квантов феномен, който няма аналог в класическата физика. В квантовата механика разделянето на общата енергия на кинетична и потенциална не е такаима смисъл, защото противоречи на принципа на неопределеността. Всъщност фактът, че частицата има определена кинетична енергия T, би бил еквивалентен на факта, че частицата има определен импулс. По същия начин, фактът, че дадена частица има определена потенциална енергия 0, би означавал, че частицата е на точно определено място в пространството. Тъй като координатата и импулсът на частицата не могат едновременно да имат определени стойности, T и U не могат да бъдат точно определени едновременно.По този начин, въпреки че общата енергия на частицата E има точно определена стойност, тя не може да бъде представена като сума от точно определени енергии T и V. Ясно е, че в този случай заключението, че T е отрицателно "вътре" в тунела, става безпочвено.