Пресечна точка на линия и повърхност
В общия случай задачата се формулира по следния начин: да се построят пресечните точки Аi на кривата t с повърхнината Ф, като задача за определяне на пресечната точка на правата и равнината.
Проблемът се решава на три етапа.
а) Кривата t се отнася за спомагателната издадена цилиндрична повърхнина Г.
в) Построена е линия m от пресечната точка на тази и спомагателната проектираща повърхнина.
в) Фиксирани са пресечните точки Аi на правите t и m, които са желаните пресечни точки.
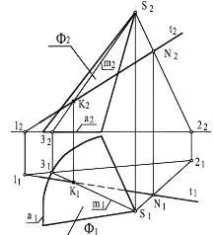
Ние илюстрираме всичко това с примера за конструиране на пресечните точки на линията t с коничната повърхност Ф (Фигура 8.29).
Целесъобразно е правата t да се отнесе към общата равнина Γ (t ∩ SN), минаваща през върха S на коничната повърхнина Φ. Тогава Γ пресича Φ по образуващата m, което значително опростява решението.
Фигура 8.29 - Пресичане
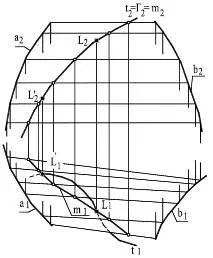
Фигура 8.30 - Пресечна точка на пространствена крива с цилиндроид
На първия етап се изгражда линия 12 на пресечната точка на равнината G с равнината на основата на коничната повърхност. След това се определя позицията на линията m. Пресечната точка на образуващата m и правата t ще определи решението - точка К.
За общия случай решението на проблема за пресичането на цилиндроид с пространствена крива е както следва (Фигура 8.30). Кривата t е затворена в челно издаден цилиндричен
повърхността Γ, която пресича цилиндроида Φ по кривата m. Тъй като m ⊂ G,
тогава неговата фронтална проекция m2 съвпада с изродената проекция Г2 на спомагателния
мощна повърхност G.
Хоризонталната проекция m1 на пресечната линия m е построена от точки от
условия за принадлежност към цилиндроида F. Правите t и m, принадлежащи на
повърхнини Г се пресичат в търсените точки L и L'.
Намаленарешението е типично. В някои случаи за по-точно
изграждане на линия на пресичане на дадена и спомагателни повърхности
или за опростяване на конструкциите е препоръчително да се използват други видове
Въпроси за сигурност за раздели 8.4 и 8.5
1. Какви са основните методи за изграждане на линия на пресичане на повърхност
сти и равнина, две повърхнини
2. Какъв е методът на режещата равнина? Рязане на сфери?
3. Кога може да се приложи методът на секущите сфери?
4. Формулирайте теоремата на Монж.
5. Назовете основните стъпки при конструирането на пресечната точка на линията и
права с конична повърхност
Литература
1. “Дескриптивна геометрия” S.A. Фролов
2. „Курс по дескриптивна геометрия” от V.S. Гордън
3. “Дескриптивна геометрия” от А.В. Бубенников
4. Учебник за висшите учебни заведения - 3-то издание, преработено и допълнено М. Висше училище 1985, 288 стр.