Приложение на интегралите
Научихме как да изчисляваме интеграли от полиноми. Това вече е достатъчно, за да можете да решите много математически и физически задачи. Като начало нека покажем как просто някои формули, изучавани в училище, се получават с помощта на интеграли.
Нека изведем формулата за пътя на равномерно ускорено движение. Ако началната скорост на тялото в момента t=0 е равна наv0,и ускорението на движение е равно на a, то в момента t скоростта на тялото ще бъдеv(t)=v0+at.Следователно, съгласно формула (3), изминатият от тялото път от началото на движението до моментаT,се изразява с формулата:
Сега извеждаме някои геометрични формули. Първо, нека намерим на какво е равен обемът на топката с радиусR.Разбира се, достатъчно е да намерим обема на полукълбото и след това да го удвоим. Нека изрежем полукълбото с равнина, успоредна на основата му и на разстояниеxот основата (фиг. 14). Напречното сечение ще бъде кръг с радиус
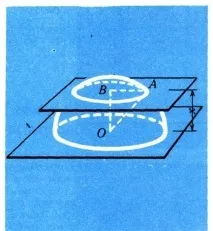
(това се получава чрез прилагане на Питагоровата теорема към триъгълникаОАВ).Следователно площта на полученото сечение е равна на:
Но тогава обемът на полукълбото (височината му еR)се изразява с формулата:
Следователно обемът на цялата топка е 4/3Pi*R 3 .
Но с помощта на интегралното смятане можете да намерите и такива области и обеми, които не се изучават в училище. Да намерим например площта на параболичния сегментAOBA, yна който хордатаABе равна на b,, а стрелкатаOCе равна наh(фиг. 15). Уравнението на парабола има форматаy=ax 2 .В точката с абсцисатаx=b/2, ординататаADтрябва да е равна на дължината на стрелкатаh.Следователно
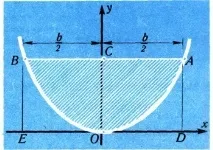
Но това означава, че
И така, нашият параболичен сегмент е ограничен отдолу от парабола, чиято ордината е в точката с абсцисатаx
Вече можем лесно да намерим площта на криволинейния триъгълникОАD.Поформули (2) и (7) е равно на:
Площта на правоъгълникаABEDе равна наbh.Но площта на параболичния сегмент се получава чрез изваждане на два пъти площта на триъгълникаОАО,от площта на правоъгълника, т.е. тя е равна на2bh/3.
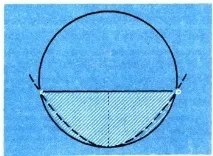
Кръгов сегмент с малък централен ъгъл може приблизително да бъде заменен с параболичен сегмент със същата хорда и същата стрелка (фиг. 16). Следователно, за площта на кръговия сегмент се извършва приблизителната формула:
Например, ако централният ъгъл е 60°, тогава приблизителната формула дава резултат 0,0893. R 2 , докато точната стойност е 0,0906...R 2 .Така, дори за такъв относително голям централен ъгъл като 60°, горната формула дава точност до 1,5%.