Примери за рекурсивни функции, Пример
Пример. (Единична изрична рекурсия)
float fact(int n);
float fact (int n)
иначе връща n факт (n_1);
Дълбочина - n+1, ширина - 1. Диаграмата на стека на повикванията е показана на фиг. 6.
Фиг.6. Диаграма на стека на повикванията
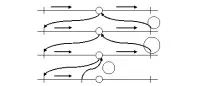
Пример. (Двойна явна рекурсия)
Изчислете функцията на Фибоначи.
Лесно е да се преброят първите членове на тази последователност.
float Fib(int n);
float Fib(int n)
връща Fib(n_1)+Fib(n_2);
Очевидно максималната дълбочина на стека за повиквания (фиг. 7) е равна на n + 1, не е лесно да се изчисли ширината на стека - долният ръб е неравен. Нека оценим ширината на стека отгоре на нивото на максималната дълбочина с числото 2 n-1 . Тогава броят на извиканите екземпляри на функцията Fib може да достигне стойността 1+2 1 +2 2 + … +2 n-1 =2 n -1.
Фиг.7. Стекова диаграма
Рекурсивните функции използватосновните изчислителни ресурси на компютъра по различни начини:памет (програмен стек)ивреме за изпълнение на програмата.
Единичната рекурсия създава дълбок стек за повиквания с една ширина и бързо запълва стека. Времето за изпълнение на програмата преди препълване на стека е незначително.
Двойната рекурсия, напротив, формира широк стек за повиквания, чиято ширина нараства експоненциално. Броят на екземплярите на една рекурсивна функция расте лавинообразно. Това води до рязко забавяне на програмата. В този случай размерът на програмния стек нараства линейно с увеличаване на дълбочината на стека.
Така че извикването на функцията Fib(50) ще извика 2 50 = 1 пентабайт екземпляри на Fib, докато програмният стек ще съдържа максимум 50·(2+4)=300 байта.
Пример. (Разпознаване на формула, написана в низ)
Формуласъдържа: реални константи, променлива x и операции "+", "-", "*", "/".
#define NO_OPERATION -1
#include …// включително заглавни файлове
синтактичен анализ на float (char *str, float x);
printf("%f", анализиране(str, 3)); // -2
синтактичен анализ на float (char * str, float x)
// функция за разделяне на низа на две части
char * substr1 = NULL, * substr2 = NULL;
// substr1 - лявата част на низа преди знака
// substr2 - дясна част след знака
char * ptr = NULL;
// y е междинна променлива за съхраняване на левия операнд,
// z е за дясно, x и y извикват анализиране рекурсивно
char op = NO_OPERATION;
// търси първото срещане на знака `+' и превежда указателя към този знак
if ((ptr = strchr (str, '+'))!= NULL)
// подобно търсене на символа `-',`*',`/', но от края на низа
друго ако ((ptr = strrchr (str, '-'))!= NULL)
друго ако ((ptr = strchr (str, '*'))!= NULL)
друго ако ((ptr = strchr (str, '/'))!= NULL)
ако (op!= NO_OPERATION)
substr1 = (char *) malloc ((int) (ptr - str) + 1);
// памет за левия подниз плюс един знак за края на низа
ако (substr1 == NULL)
printf(" ГРЕШКА: Няма памет. ");
substr2 = (char *) malloc (strlen(str) - (int) (ptr-str));
// памет за десния подниз
ако (substr2 == NULL)
printf("ГРЕШКА: Няма памет. ");
// запис на първите ptr-str знаци в substr1...
// ...низът str и краят на низа
strncpy (substr1, str, (int) (ptr-str));
// запис в substr2 започвайки от ptr+1 до края на str
strcpy(substr2,ptr+1);
y = синтактичен анализ(substr1, x);
// изчисляване на формулата на левия подниз
z = синтактичен анализ(substr2, x);
// изчисляване на правилната формула за подниз
case DIV: if (z == 0)
printf("Деление на нула");
друго ако (! strcmp (str, "x"))
// str съвпада с "x", връща x
// str съдържа само реална константа
върни atof(str);
Диаграмата на стека на повикванията е показана на фиг. 8. Първите четири кръста са условията за излизане от парсинг, петият кръст е съвпадението на низа с "x" и връщане x, третият кръст е съвпадението на низа с реална константа и връщане atof(str). Първият кръг е y, вторият е z. операция между тях. Дълбочината на стека е n, където n+1 е броят на операциите.
Фиг.8. Стекова диаграма
По този начин имаме изрична двойна рекурсия.
Недостатъци на разглежданата парсинг функция.
- За някои низове двойната рекурсия се изражда в единична рекурсия. Например, за низа "x+x+x+x+x+x+x+x", диаграмата на стека на повикванията ще има дълбочина 7 и ширина винаги 2. В резултат на това стекът ще бъде задръстен. По-добре е да търсите средна операция. Тогава двоичното дърво на стека на повикванията ще бъде балансирано.
- Функцията за анализиране за всяко x ще създаде двоично дърво на стека на повикванията. Това може да доведе до забавяне на изчислението, например при изчертаване на графики. По-добре е да изградите междинен низ, съдържащ полската форма на формулата веднъж по рекурсивен начин. След това формулата ще бъде оценена върху междинния ред за всяко x, нерекурсивно.