Прогнозиране на базата на линейна регресия
Работни страници

Съдържанието на произведението
ЛАБОРАТОРИЯ #4
ПРОГНОЗИРАНЕ С ЛИНЕЙНА РЕГРЕСИЯ
Използвайки уравнение на линейна регресия, можете да предвидите стойността на зависимата променлива за определена стойност xp на независимата променлива. Тъй като не знаем точното регресионно уравнение, не можем да направим точна прогноза. Може само да се твърди, че индивидуалната стойност на y за даден x ще попадне в доверителния интервал с вероятност g.
Вероятността g се нарича ниво на надеждност.

Краищата на доверителните интервали са разположени в краищата на хиперболата (доверителните граници) при ниво на надеждност g. Дължината на доверителния интервал е минимална при . Тъй като xp се отдалечава от, доверителният интервал се увеличава, следователно прогнозата, използваща уравнението на примерната регресия, става по-малко точна. Следователно, прогнозирането на стойностите според регресионното уравнение е оправдано, ако xp не надхвърля диапазона от стойности (хmin, xmax). Този интервал е прогнозната зона.
Полуширината на доверителния интервал се изчислява по формулата:
Syp - стандартна грешка на прогнозата
е стандартната грешка на регресията.
t е критичната стойност на t-статистиката;
a = 1-g - ниво на значимост;
R=n-2- брой степени на свобода.
Точността може да се оцени с помощта на относителната грешка на прогнозиране.
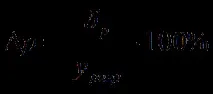
Задача:използване на данни от лаборатория 1:
- Намерете уравнение на линейна регресия
- Изчислява се полуширината на доверителния интервал за всички пробни точки, както и за две зададени точки от прогнозната област с ниво на надеждност 0,95.
- Намерете относителната грешка на прогнозата за ниво на надеждност от 0,95.
- Начертайте регресионната линия с доверителни граници при g=0,95.
Изчисленията се правят в следната форма:
Прогноза на линейния модел