Производната на частното и произведението – формула за две функции

Производната или функцията в точка е основната концепция в диференциалното смятане, тя характеризира скоростта на промяна на функция в дадена точка. Може да се дефинира като границата на съотношението на трансформациите на функцията към увеличението на нейния аргумент, тогава този аргумент клони към нула (ако границата съществува). Функция, диференцируема в дадена точка, е функция, която има крайна производна в дадена точка.

Ако функциитеu = u(x) иv=v(x) имат производна в точкатаx, тогава тяхното частно, при условие чеv(x) ≠ 0 има производна в точката:

Ако функциитеu1(x), u2(x), u3(x), …. , un(x) имат производни в точкатаx, тогава функциятаy = u1(x) u2(x) u3(x) … има производна в тази точка. un(x) иу´ = u1´ u2 u3… un+ u1

Готфрид Лайбниц

немски философ, логик, математик, физик, юрист, историк, дипломат, изобретател и лингвист

u2´ u3… un+….+ un´ u1 u2 u3 … un-1. След като разделим тези две части на функциятаuv получаваме:

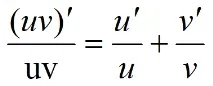
Чрез примера ще намерим производната на функциятаy(x) = за решението, просто трябва да замените стойностите на това във формулите в уравнението:

---