Ръчно изчисление - страница 4
Пример за минимизиране на получените изрази
x 1 x 2 x 3 x 4
Както вече беше отбелязано, простият импликант абсорбира част от съставната част на единицата, ако е нейна собствена част. Съответната клетка на импликантната матрица в пресечната точка на реда (с разглеждания прост импликант) и колоната (с единичната съставна част) е отбелязана с кръст (Таблица 4.1). Минималните DNF се конструират от импликантната матрица, както следва:
1. Търсене на колони от импликантната матрица, които имат само един кръст. Простите импликанти, съответстващи на тези кръстове, се наричат основни импликанти и представляват така нареченото ядро на булевата функция. Ядрото е задължително включено в минималния DNF.
2. Разглеждат се различни варианти за избор на набор от прости импликанти, които ще покрият с кръстове останалите колони от импликантната матрица, и се избират опции с минимален общ брой букви в такъв набор от импликанти.
По този начин минималният DNF ще изглежда така:
F ( X 1 , X 2 , X 3 , X 4 ) X 1 X 2 X 3 X 1 X 3 X 4 X 1 X 2 X 3 .
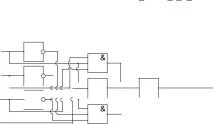
Използвайки изразите, получени по време на минимизиране, ние конструираме устройство, което реализира дадената таблица на истината (фиг.).
F (X 1, X 2, X 3, X 4) X 3
В заключение отбелязваме, че перфектните нормални форми не са най-лесният начин за дефиниране на превключващи функции. Като правило те позволяват трансформация с помощта на правилата на булевата алгебра до по-проста форма. Един от следващите раздели на курса е посветен на методите за конструиране на най-простите представяния на превключващи функции.
Въпроси за самопроверка
1. Използвайки таблицата на истината (Таблица 4.2), минимизирайте получения израз с помощта на SDNF.
Таблица със задачи за самостоятелна подготовкаработа
F 1 ( X 1 , X 2 , X 3 )
F 2 ( X 1 , X 2 , X 3 )
F 3 ( X 1 , X 2 , X 3 )
F 4 (X 1, X 2, X 3)
F 5 (X 1, X 2, X 3)
2. В софтуерния пакет CAD изградете получената диаграма на устройството.
3. Покажете принципа на неговото действие, като използвате пример.
Въпроси за самоконтрол
1. Какво е перфектна дизюнктивна нормална форма?
2. Какво е перфектна конюнктивна нормална форма?
3. Дайте пример за операцията залепване и попиване.
4. Етапи на преобразуване на функция по метода на Куайн?
5. Как се избират основните импликанти?
5. ИЗСЛЕДВАНЕ НА КОМБИНИРАНИ ЦИФРОВИ УСТРОЙСТВА. ТРИГЕРИ
Целта на главата: изследване на комбинирани цифрови устройства - тригери. Съставяне на таблици на истинност и тяхното конструиране на базата на прости логически функции.
Тригер (тригерна система) е един от основните (основните) елементи на цифровата техника. Под тригер разбираме устройство от сериен тип с две стабилни равновесни състояния, предназначено за запис и съхраняване на информация. Под действието на входните сигнали тригерът може да преминава от едно стабилно състояние в друго. В този случай напрежението на изхода му се променя рязко.
Отличителна черта на тригера като функционално устройство е свойството да съхранява двоична информация. Под тригерна памет се има предвид способността да се остане в едно от двете състояния дори след прекратяване на превключващия сигнал. Вземайки едно от състоянията като "1", а другото като "0", можем да предположим, че тригерът съхранява (помни) един бит от число, записано в двоичен код. При две последователни превключвания на тригера се формира един импулс на изхода, т.е. тригерът може да се използва като делител на честотакомутационни сигнали с коефициент равен на две.
При производството на джапанки се използват предимно полупроводникови устройства (обикновено биполярни и полеви транзистори), в миналото - електромагнитни релета, вакуумни тръби. Понастоящем логическите схеми, включително тези, използващи тригери, се създават в интегрирани среди за разработка за различни програмируеми на място логически интегрални схеми (FPGA). Те се използват главно в компютърните технологии за организиране на компонентите на компютърните системи: регистри, броячи, процесори, памет.
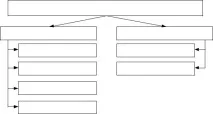
Джапанките могат да бъдат разделени на две групи: без тактова честота и с тактова честота. Нетактовият (асинхронен) тригер може да промени състоянието си чрез превключване на сигнали по всяко време. Тактовият (синхронен) тригер се превключва синхронно с пристигането на специален тактов импулс. Блоковата диаграма е показана на фигура 5.1.