Реализиране на алгоритъма за оптимизиране на параметрите на молекулярно-динамичния потенциал REAXFF
Публикационна дейност
Номер на следващия сайт
Реализиране на алгоритъма за оптимизиране на параметрите на молекулярно-динамичния потенциал REAXFF
Численото моделиране на химически реактивни молекулни системи е от значение за редица приложни научни проблеми. За малки химични съединения (до 100 атома) това може да се направи чрез методите на квантовата механика (ab initio), но тези методи са неподходящи за моделиране на по-големи структури поради високата си ресурсоемкост. Традиционните методи на молекулярната динамика, които обикновено се използват за широкомащабни системи, обикновено се основават на класическия потенциал на силовите полета и не позволяват добре възпроизвеждане на многокомпонентни химически реактивни системи. Ето защо в нашата работа, свързана с изследването на системи за съхранение на водород, ние използваме комбиниран подход за симулиране на разрушаването на леки метални хидриди с освобождаване на водород. Базира се на потенциала на реактивните силови полета ReaxFF (Reactive Force Field) [1, 2], чието параметризиране се извършва на базата на точни квантови изчисления за малки клъстери. Трябва да се отбележи, че потенциалът на ReaxFF първоначално е разработен, за да опише химическа реактивност, дисоциация и образуване на химични връзки, дефекти, повърхностни ефекти и т.н. Този подход позволява да се симулират системи, развиващи се във времето с броя на атомите от порядъка на 106–108 на модерни високопроизводителни паралелни изчислителни клъстери.
ReaxFF потенциал. Формата на MD потенциала ReaxFF е подобна на тази, използвана в много нереактивни силови полета, където енергията на системата се състои от различни енергийни приноси. Основната разлика се състои в използването не на метод на твърдо обвързване, а на методпоръчки за свързване. Редът на връзката характеризира множеството връзки между определена двойка атоми в съединение и се изразява с формулата
,
където индексът l е равен на σ, π, ππ (видове ковалентна връзка); rij е разстоянието между атомите; pl1, pl2, rl са параметри [2]. Поръчките на връзките, изчислени в числени симулации за всички атоми директно от междуатомни разстояния и актуализирани на всяка времева стъпка, позволяват да се опише образуването и дисоциацията на връзките по време на симулация. Общата форма на потенциала [2] е следната:
+Econj+Ehbond+Elp+ EvdWaals+ECoulomb. (1)
Всеки член от дясната страна на формулата е отговорен за отделен тип взаимодействие: ковалентно (характеризирано с реда на химичните връзки, термини Ebond, Eover, Eunder), тричастици (ъгли на връзката, Eval, Epen, Ecoa), четиричастици (ъгли на двустенна връзка, Etors, Econj), Кулон (ECoulomb), ван дер Ваалс (EvdWaals), водородни връзки ( Ehbond) и енергийно кодирани електронни двойки (Elp).
Общата енергия е сумата от функциите на относителните позиции на атомните двойки rij, тройките rijk и четворките rijkl. Освен това всяка от тези функции зависи от редица параметри, които се определят от това кои химични елементи взаимодействат. По този начин целият потенциал зависи от множество (в зависимост от сложността на връзката техният брой може да бъде повече от 100) параметри: EReaxFF=f(p1, p2, p3, …, pN). Анализът на подробната форма на всички членове във формула (1) ни позволява да заключим, че EReaxFF и нейното първо производно са непрекъснати функции на атомните координати дори при химични реакции [2].
Метод за еднопараметърна оптимизация. Реализацията на алгоритъма за оптимизиране на параметрите се основава на метода за еднопараметърно търсене [5]. Данните, по коитотърсене (оптимизиращ набор, набор за обучение) се получават от изчисления на прости модели на химични съединения (до 50 атома) с помощта на методи на квантовата химия или се вземат от експеримента. Данните за оптимизация са геометричните характеристики на молекулите (разстояния между атомите, ъгли на свързване, двустенни ъгли), честоти на вибрации, ефективни заряди на атоми и енергии на свързване на съединенията, както и всякакви други характеристики, които могат да бъдат изчислени чрез методи на молекулярната динамика и след това сравнени с данните от оптимизиращия набор. Процедурата за търсене с един параметър се състои в промяна на параметрите на потенциала за минимизиране на сумата от квадрати:
(2)
Тук xiQC/Lit са данни от оптимизиращия набор (специфични характеристики на модела или молекулата, получени чрез методи на квантовата химия или от литературата (експеримент)); xiReaxFF - изчислено с помощта на стойности на ReaxFF, съответстващи на тези характеристики; σi е критерият за приемане, който има размерността xi и характеризира приноса на разликата xiQC/Lit–xiReaxFF към сумата от квадрати. Сумата (2) е така наречената функция на грешката - отклонението на изчисленията на ReaxFF от данните на оптимизиращия набор. Всеки xiReaxFF зависи от потенциалните параметри p1, . pN, така че Err е функция на тези параметри.
Важно е да се отбележи, че за да се изчисли стойността на xiReaxFF за всеки модел на оптимизиращия набор за специфични стойности на параметри, е необходимо да се търси минималната потенциална енергия (1) на този модел като функция на координатите на съставните му атоми, като се използва някакъв многопараметричен метод, например методът на спрегнат градиент. Тази процедура не трябва да се бърка с процедурата за минимизиране на сумата (2) като функция на потенциалните параметри.
Основата на метода за еднопараметрична оптимизацияе параболична екстраполация, която се извършва последователно за всеки параметър pk, като останалите са фиксирани. На малки интервали зависимостта между грешката Err и стойността на всеки параметър pk може да се счита за параболична, следователно, за да се определи оптималната стойност на параметъра, е необходимо да се изчисли Err за три различни стойности: pk, pk(1–δk), pk(1+δk), където δk
Една итерация на програмата се състои в изпълнение на описаната процедура веднъж за всеки pk от списъка. Тъй като повечето от параметрите в силовото поле ReaxFF са свързани, оптималната стойност на всеки параметър се измества при всяка промяна на друг параметър. Това означава, че процесът на оптимизация трябва да се повтаря, докато Err спре да намалява, което се определя от критерия за конвергенция ε. Обърнете внимание, че за всеки параметър pk трябва да бъде определен валиден интервал на вариация [Dkmin, Dkmax], за да се избегне сближаване в нереалистична област.
Трябва също да се отбележи, че еднопараметърният метод за търсене гарантира конвергенция до минимум, но този минимум може да не е абсолютен, а само локален.
Описание на програмата за оптимизиране на потенциалните параметри ReaxFF. Блоковата схема на алгоритъма на разработената програма е показана на фигурата. Общата структура на програмата включва инициализация, четене на входни данни, два вложени цикъла, запис на междинни и изходни резултати. Външният цикъл организира итерации върху пълния набор от параметри, а вътрешният осигурява процедурата за екстраполация на параметъра pk. Вътрешният цикъл съдържа изчисления с потенциала на ReaxFF на всички модели от набора за оптимизация и изисква много ресурси. Той е паралелен с помощта на MPI технология, която ви позволява да стартирате програмата на изчислителните възли на клъстера.
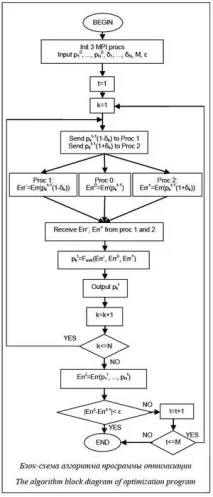
Външният цикъл итерира набор от параметри. В една стъпка от този цикъл е възможно да преминете през целия списък p1, . pN, като за всеки pk се извършва една процедура на екстраполация. Резултатът от една итерация е нов набор, който ще бъде използван в следващата итерация. Цикълът завършва, ако условието за конвергенция Errt–Errt-1 е изпълнено на следващата стъпка t
На изхода на програмата се получават два текстови файла: файл с оптимизирани потенциални параметри и лог файл (дневник на работата на програмата). Дневникът на програмата съдържа подробна информация за всички итерации на вътрешния цикъл. При всяка итерация в него се записва името на параметъра; неговите три значения; грешки (2) на тези стойности; коефициенти на екстраполационна парабола; екстремум на параболата; стойност на параметъра, получена чрез екстраполация; екстраполирани и изчислени стойности на грешките на параметрите; крайната стойност на параметъра, избрана за оптимална; неговата грешка (2).
Дневникът ви позволява да контролирате напредъка на процеса на оптимизация, ако е необходимо, да спрете програмата и да продължите изпълнението й от произволна итерация.
Структура на опаковката. Изходният код на програмата е разработен на език C и има модулна структура. Софтуерният пакет е сглобен и достъпен катоархив с изходни кодове, инструкции и скрипт за компилация, документация за потребителя и примери за входни файлове.
Тестване и използване. Функционалността на програмата беше тествана на примера за оптимизиране на параметрите на алуминия и неговите хидриди. Параметрите, включени в комплекта за разпространение на пакета LAMMPS, бяха взети като първоначално приближение по време на оптимизацията, което трябва да се счита за доста грубо, тъй като те дават лоши резултати за решетки от метал и неговите хидриди.
За оптимизиране на параметрите използвахме набор, който включва чисти алуминиеви клъстери (Al2 – Al8, Al13), хидридни клъстери (AlnH3n, n=1, .8), както и кристали от α-β- и γ-модификации на алуминиев хидрид [6, 7], генерирани от клетки с периодични условия. Добавянето на безкрайни кристални структури към набора направи възможно да се вземе предвид уравнението на състоянието, тоест зависимостта на кристалната енергия от обема на клетката. Общо комплектът включваше 56 структури.
Общо 79 потенциални параметъра бяха включени в оптимизацията. Една итерация на процедурата за оптимизация (за един параметър) на изчислителния клъстер отне около 4 часа в този случай. За една итерация стойността на грешката намалява със стойност от 0,1 до 1% в сравнение с предишната итерация. Програмата направи около 4000 итерации, през което време грешката беше намалена с около 500 пъти.
За да се провери качеството на получените параметри, кристалните решетки на алуминиеви хидриди бяха симулирани при първоначални и оптимизирани параметри, за да се сравни тяхната стабилност, плътност и структурна редовност при стайна температура. Всички първоначални решетки бяха синтезирани според изчисленията на квантовата химия за всяка от модификациите; всяка система съдържа около 4000 атома и е поставена във вакуум. ЧисленЕкспериментът се състоеше в наблюдение на поведението на всяка система във времето при постоянна температура (300 K), поддържана от термостат Nose-Hoover.
При моделиране с първоначалния набор от параметри кристалната структура на всички хидриди се разпада и плътността на веществото намалява почти два пъти. При оптимизирания набор от параметри правилната структура беше напълно запазена, въпреки че константите на кристалната решетка се промениха леко (1–6%). В края на експеримента кристалните плътности при оптимизираните параметри се различават от реалните съответно с 9, 14 и 4% за α-, β- и γ-модификациите.
По този начин разработената програма за търсене на параметрите на потенциала ReaxFF е доста универсална и може да се използва за системи от атоми от произволен тип. Наборът за оптимизиране може да включва всякакви съединения, въпреки че наборът от характеристики на тези съединения все още е ограничен: той включва дължини на връзките, ъгли на връзката и ъгли на двустенна връзка, енергии на атомизация, топлина на образуване и ефективни атомни заряди. Модулната структура на кода улеснява добавянето на разширения за приспособяване на допълнителни условия или характеристики на модела. Беше демонстрирана приложимостта на разработените методи за оптимизиране на параметрите на ReaxFF потенциала за MD моделиране на алуминиеви хидриди.