Решаване на задачи с разклоняващи се алгоритми
Решаване на задачи с линейни алгоритми.
Линеен се нарича алгоритъм, при който всички етапи на решаване на проблема се изпълняват строго последователно. Това означава, че не съдържа проверки на условия и повторения.
Блоковата схема на алгоритъма изглежда като последователност от действия.
Графичният начин за описание на алгоритъма (блокова диаграма) е най-широко използван. За графично описание на алгоритми се използват схеми на алгоритми или блокови символи (блокове), които са свързани помежду си чрез комуникационни линии.
Всеки етап от изчислителния процес е представен с геометрични фигури (блокове). Те са разделени на аритметични или изчислителни (правоъгълник), логически (ромб) и входно-изходни блокове за данни (успоредник).
Задача 1.Определете разстоянието в равнината между две точки с дадени координати M1(x1,y1) и M2(x2,y2).
Дадена е блокова диаграма, за да разрешите проблема, напишете програма на псевдокодове
Направи го сам
Задача 2.Съставете линейна програма под формата на блокова диаграма и в псевдокод, за да разрешите следния проблем:
Вариант 1.Дадена е дължината на ръба на куб. Намерете обема на куб и неговата странична повърхност.
Вариант 2.Обиколката е известна. Намерете площта на кръга, ограден от този кръг.
Вариант 3.Изчислете височината на триъгълника, спуснат до странатаа, като използвате известните стойности на дължините на страните муa, b, c.
Вариант 4.Въз основа на дадените страни на правоъгълника изчислете неговия периметър, площ и дължина на диагонала.
Решаване на проблеми с разклонени алгоритми
В практиката често има проблеми, при които в зависимост от началните условия или междинните резултати е необходимо да се извършат изчисленияедна или друга формула.
Такива проблеми могат да бъдат описани с помощта на алгоритми за разклонена структура. В такива алгоритми изборът на посоката на продължаване на изчислението се извършва въз основа на резултатите от проверката на дадено условие. Процесите на разклоняване се описват от израза IF (IF условие).
Решаването на много задачи се характеризира с многократно повторение на отделни раздели на изчисленията. За решаване на такива проблеми се използват алгоритми с циклична структура (циклични алгоритми).
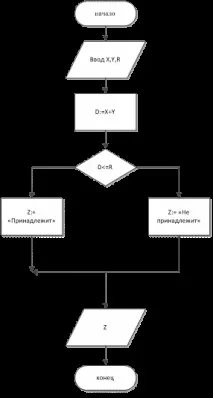
Задача 3.Дадени са цели числа X, Y. Определете дали точка с координати X, Y принадлежи на окръжност с радиус R.
Покажете съобщението „Притежаван“ или „Не притежаван“.
Дадена е блокова схема. Напишете алгоритъм в псевдокод
.
Направи го сам
Задача 4.Съставете алгоритъм за задачата под формата на псевдокодове и блокова схема.
Вариант 1. Напишете програма, която изпълнява епизод от приказка: машината пита къде ще отиде героят и в зависимост от отговора (наляво - (-1), направо - 0, надясно - 1), отпечатва какво ще се случи с героя.
Вариант 2.Морска битка. Машината измисля две числа от 0 до 9. Играчът се опитва да ги познае, като въвежда своите две числа. Ако съвпаднат (в която и да е комбинация), тогава играчът печели.
Вариант 3.Корабът Корабът търпи бедствие в Атлантическия океан.
Всички пътници ще бъдат спасени, ако два кораба се притекат на помощ. Корабът ще остане на повърхността2часа. Скоростта на спасителните кораби е 40 възела/ч. Направете програма, която определя дали пътниците ще бъдат спасени.
Известните разстояния на спасителни кораби до потъващ кораб са 30 км и 45 км
Възел - морска миля на час - мярка за скорост. Но в една миля - 1852 метра.часа.
Вариант 4.През стария мост тече потокавтомобили. 3 коли могат да бъдат на моста едновременно. Ако 3 коли или 2 коли и камион се качат на моста, мостът ще издържи, в други случаи ще се срути.