Решете системата 6 клас, математика-повторение
За да решите система от линейни уравнения с две променливи, като използвате метода на добавяне, трябва:
1) умножете лявата и дясната част на едното или двете уравнения по определено число, така че коефициентите за една от променливите в уравненията да станат противоположни числа;
2) съберете получените уравнения член по член и намерете стойността на една от променливите;
3) заместете намерената стойност на една променлива в едно от тези уравнения и намерете стойността на втората променлива.
Ако в дадена система коефициентите за една променлива са противоположни числа, тогава ще започнем решаването на системата веднага от точка 2).
Примери. Решете система от линейни уравнения с две променливи, като използвате метода на събиране.
Тъй като коефициентите при y са противоположни числа (-1 и 1), започваме решението от точка 2). Събираме уравненията член по член и получаваме уравнението 8x = 24. Всяко уравнение на оригиналната система може да бъде написано като второто уравнение на системата.
Намерете x и заменете стойността му във второто уравнение.
Решаваме второто уравнение: 9-y \u003d 14, следователно y \u003d -5.
Нека направимпроверка. Заместете стойностите x = 3 и y = -5 в оригиналната система от уравнения.
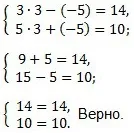
Отговор: (3; -5).
Ако умножим първото уравнение по (-2), тогава коефициентите за променливата x ще станат противоположни числа:
Събираме тези равенства член по член.
Ще получим еквивалентна система от уравнения, в която първото уравнение е сумата от две уравнения на предходната система и ще напишем 1-вото уравнение на оригиналната система като 2-ро уравнение на системата (обикновено те пишат уравнението с по-малки коефициенти):
Намеретеy от първото уравнение и получената стойностзаместваме във 2-ро.
Решаваме последното уравнение на системата и получаваме x = -2.
Отговор: (-2; 1).
Нека направим коефициентите на променливатаy противоположни числа. За да направим това, умножаваме всички членове на първото уравнение по 5 и всички членове на второто уравнение по 2.
Заместете стойността x=4 във второто уравнение.
3 4 - 5y = 27. Нека опростим: 12 - 5y = 27, следователно -5y = 15 и y = -3.
Отговор: (4; -3).
6.9.2. Решаване на системи от линейни уравнения по метода на заместването
За да решим система от линейни уравнения с две променливи, като използваме метода на заместване, процедираме както следва:
1) изразяваме една променлива чрез друга в едно от уравненията на системата (x през y или y през x);
2) заместваме получения израз в друго уравнение на системата и получаваме линейно уравнение с една променлива;
3) решаваме полученото линейно уравнение с една променлива и намираме стойността на тази променлива;
4) намерената стойност на променливата се замества в израз (1) за друга променлива и намираме стойността на тази променлива.
Примери. Решете система от линейни уравнения, като използвате метода на заместване.
Нека изразимx през y от първото уравнение. Получаваме: x \u003d 7 + y. Нека заместим израза (7+y) вместоx във второто уравнение на системата.
Получихме уравнението: 3· (7+y)+2y=16. Това е уравнение с една променливаy. Ние го решаваме. Нека отворим скобите: 21+3y+2y=16. Събираме термините с променливатаy от лявата страна и свободните термини отдясно. Когато прехвърляме член от една част на равенството в друга, променяме знака на члена на противоположния.
Получаваме: 3y + 2y \u003d 16-21. Във всяка част от равенството даваме еднакви членове. 5y=-5. Разделяме двете страни на равенството на коефициента на променливата. y=-5:5; y=-1. Заменете тази стойностy в израза x=7+y и намеретеx. Получаваме: x=7-1; х=6. Двойка променливи стойности x=6 и y=-1 е решението на тази система.
Запишете: (6; -1). Отговор: (6; -1). Удобно е да напишете тези аргументи, както е показано по-долу, т.е. системи уравнения - вляво една под друга. Вдясно - изчисления, необходими обяснения, проверка на решението и др.