Резюме Математическа изчислителна система MATLAB - Банка от резюмета, есета, доклади, курсови работи и
Изчисляване на корен квадратен от матрица и матричен експонент
За неособени квадратни матрициA, функциятаsqrtmизчислява главната стойност на квадратния корен, т.е. акоX = sqrtm(A), тогаваX*X = A.Букватаmвsqrtmозначава, че се извършва матрична операция. Това отличава тази функция отsqrt(A),, която, подобно наA.^(1/2)(обърнете внимание на точката!) изпълнява операцията за извличане на корен елемент по елемент.
Системата от обикновени линейни диференциални уравнения от първи ред може да бъде записана като
къдетоx = x(t)е векторна функция наt,иAе постоянна матрица, независима отt.
Решението на тази система може да се изрази като матричен показател.
Функциятаexpm(A)изчислява експонентата на матрицата. Помислете за пример на система от диференциални уравнения със следната 3x3 матрица от коефициенти
и начални условияx(0)
Използването на матричния показател за изчисляване на решението на диференциално уравнение при 101 точки със стъпка от 0,01 в интервала 0 ≤ t ≤ 1 се записва като
за t = 0 : 0,01 : 1
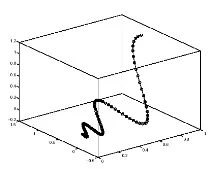
Триизмерна графика на решението във фазовото пространство може да се получи с помощта на специална функция
Решението има формата на спираловидна функция, която се сближава към началото (вижте фигурата по-долу). Такова решение се дължи на комплексните собствени стойности на матрицата на коефициентаA.
Собствени стойности и собствени вектори
Собствената стойности собственият вектор на квадратната матрицаАса скаларътλи векторътv, отговарящи на условието
С диагонална матрицаΛ,съставена от собствени стойностиλна матрицаAи матрицаV, съставена от съответните собствени векториv,могат да бъдат записани
Ако матрицатаVе неособена, въз основа на този израз, получаваме спектралното разлагане на матрицатаA
Добър пример за използването на спектралното разлагане е дадено от матрицата на коефициентите на линейно диференциално уравнение, разгледано по-горе. Въвеждане на израз
дава следния колонен вектор от собствени стойности (две от тях са комплексно спрегнати)
Реалните части на всички собствени стойности са отрицателни, което гарантира стабилността на процесите в системата. Ненулевите въображаеми части на комплексно спрегнатите собствени стойности определят осцилаторния характер на преходните процеси.
С два изходни аргумента функциятаeigсъщо изчислява собствени вектори и връща собствените стойности като диагонална матрица
-0,3553 -0,2110 - 0,6447i -0,2110 + 0,6447i
0 -2.4645+17.6008i 0
0 0 -2.4645-17.6008i
Първият собствен вектор (първата колона на матрицатаV)е реален, а другите два са комплексно спрегнати. И трите вектора са нормализирани по дължина, т.е. тяхната евклидова нормаnorm(v,2)е равна на единица.
МатрицаV*D*inv(V), която в по-сбита форма може да бъде написана катоV*D/V, е равна, в рамките на грешките на закръгляване, на матрицаA. По подобен начинinv(V)*A*VилиVA*Vе равно, в рамките на грешките на закръгляване, на матрицатаD.
Някои матрици нямат спектрално разлагане. Такива матрици се наричат дефектни или недиагонализирани. Например, нека матрицатаAизглежда така
За тази матрица входът[V, D] = eig(A)дава
0,8127 0,8165 0,8165
Тук има две положителни единични множествени собствени стойности. Втората и третата колона на матрицатаVса еднакви и следователно няма пълен набор от линейно независими собствени вектори (и следователно няма обратна матрицаV-1).
Разлагане на сингулярни стойности на матрици
Особена стойност и съответните сингулярни вектори на правоъгълна матрицаAса скаларσи двойка векториuиv, така че отношенията
Имайки диагонална матрица с единична стойностΣи две ортогонални матрициUиV, образувани от съответните собствени вектори, можем да запишем
Тъй катоUиVса ортогонални матрици, това може да се запише като разлагане на сингулярна стойност
Пълното разлагане на сингулярна стойност на mxn матрицаAвключва mxn матрицаU, mxn матрицаΣи nxn матрицаV. С други думи, и двете матрициUиVса квадратни и матрицатаΣима същия размер катоA. АкоAима много повече редове отколкото колони, получената матрицаUможе да бъде доста голяма, но повечето от нейните колони се умножават по нули вΣ. В такива ситуации може да се използва така нареченото икономично разлагане, което спестява както време, така и памет, чрез извеждане на mxn матрицаU, nxn матрицаΣи същата матрицаV.
пълното разлагане на сингулярна стойност е дадено във формата