Сфера, вписана в цилиндър, конус и пресечен конус
Определение.Сфера се наричавписана в цилиндър,конус,пресечен конус, ако всяка образуваща на цилиндъра, конуса, пресечения конус е допирателна към сферата и всяка основна равнина на цилиндъра, конуса, пресечения конус докосва сферата в точка, разположена вътре в основата.
В този случай те казват, че близо до сферата са описани цилиндър, конус, пресечен конус.
Теорема 1.Има сфера, вписана в конус.
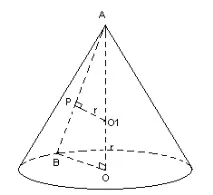
Трябва да докажем, че една сфера може да бъде вписана в конус. Тъй като знаем, че конусът е симетричен по отношение на всяко сечение, минаващо през неговата височина, тогава ако докажем, че окръжност може да бъде вписана във всяко такова сечение (центърът на всички окръжности е един и същ), тогава ще докажем, че сфера може да бъде вписана в конус.
Да разгледаме сечение от конус, минаващо през височината на конуса.
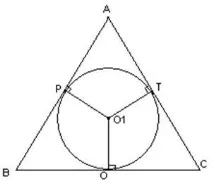
Напречното сечение на конуса е равнобедрен триъгълник с основа BC. Височината OA също ще бъде ъглополовяща. Следователно центърът на вписания кръг O1 ще бъде разположен на OA (можете, както знаете, да впишете кръг във всеки триъгълник). И тъй като всички останали разглеждани секции ще бъдат равни на ABC, тогава центровете на вписаните кръгове ще съвпадат. Това означава, че сфера с център O1 и радиус 001 може да бъде вписана в конус.
Теорема 2.Сфера може да бъде вписана в цилиндър тогава и само ако нейната височина е равна на диаметъра на основите.
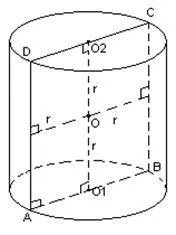
Тук разглеждаме секции, които ще бъдат правоъгълници. Окръжност може да бъде вписана само в квадрат, оттук и условието височината да е равна на диаметъра на основата.
Теорема 3.Сфера може да бъде вписана в пресечен конус тогава и само ако нейната образуваща е равна на сбора от радиуситеоснования.
Ключови задачи.
Задача 1.Има две еднакви топки с радиус R, които се докосват външно и равнината. Намерете разстоянието между допирните точки на топките и равнината.
Да разгледаме сечение, перпендикулярно на равнината, върху която лежат топките. Тъй като тези топки се допират една до друга, има равнина, която те докосват в точката K. Тази равнина ще бъде перпендикулярна на първата равнина. Следователно ъглите AO1K и KO2B са прави ъгли и следователно ABO2O1 е правоъгълник. Следователно AB=2R.
Задача 2.Две топки с радиуси R1 и R2 лежат на равнината и се допират външно. Намерете разстоянието между допирните точки на топките и равнината.
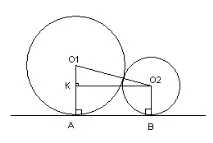
Да разгледаме сечение, перпендикулярно на равнината, върху която лежат топките. Точките A и B са допирните точки между топките и равнината. Нека пуснем перпендикуляра O2K към AO1. KO1= AO1-KA. Ако вземем предвид, че КА=О2В=R2, а О1О2=R1+R2 то според Питагоровата теорема. И тъй като KABO2 е правоъгълник, тогава KA \u003d AB, Следователно