Скорости и ускорения на точки при сферично движение, Лекции и примери за решаване на задачи по механика
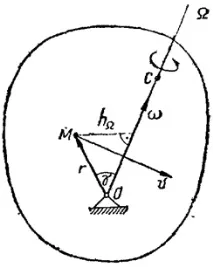
Скоростите на точките на твърдо тяло, извършващо сферично движение във всеки момент от времето, се определят като техните скорости на въртене по време на въртене около моментната осΩ(Фигура 3.4).
Познавайки положението на моментната ос на въртенеΩи ъгловата скорост на тялотоω, е възможно да се определи скоростта на всяка точка от тялотоMкато скоростта на тази точка при въртеливо движение около моментната ос, като се използва добре известната формула
къдетоrе радиус векторът на точкатаM, начертан от фиксираната точкаO.
къдетоhΩе разстоянието на точката от моментната ос на въртене.
Нека представим подвижнаOxyzи фиксиранаOx1y1z1координатни системи, подобни на Фигура 3.1.
За проекции на скоростта на точка върху неподвижна и подвижна ос се получават формулите на Ойлер:
- за фиксирана координатна система
- за подвижна координатна система
От формули (4), (5) могат да се получат уравненията на моментната ос в неподвижни и подвижни координатни системи, като се зададат всички проекции на скоростта равни на нула за точки, лежащи на моментната ос.
- За фиксирана координатна система:
- За подвижна координатна система:
Ако положението на моментната осΩвече е установено, тогава за да се намери ъгловата скоростωе достатъчно да се знае скоросттаνна всяка точкаM, която не лежи на моментната ос (Фигура 3.4).
След това, пускайки перпендикуляраhΩот тази точка върху моментната осΩ, получавамеν = ω ⋅ hΩ, откъдето
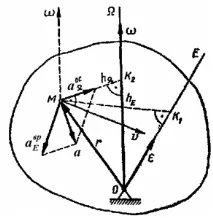
За определяне на ускорението на точка на твърдо тяло се използватеоремата на съперниците:ускорението на всяка точка на твърдо тяло по време на сферично движение се определя катогеометричната сума на неговите ротационни и осцилиращи ускорения
Модулите на тези ускорения (Фигура 3.5)
къдетоhEе разстоянието от точката до оста на ъглово ускорениеE,
hΩ— разстояние от точката до моментната осΩ.
Модулът на ускорение на точка може да се намери като диагонал на успоредник:
При сферично движение осцилиращото ускорениеaΩ osе насочено по перпендикуляра, спуснат от точката към моментната осΩ, а въртеливото ускорениеaE vрсе оказва перпендикулярно на равнината, минаваща през вектора на ъгловото ускорениеεи радиус вектораr.
Посоката на въртеливото ускорение не е същата като посоката на скоросттаν.